题目内容

6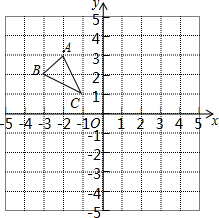．如图，在平面直角坐标系中，先画出△ABC关于y轴对称的△A′B′C′，并求出△A′B′C′的面积．

分析 首先找出A、B、C三点关于y轴的对称点A′、B′、C′，再画出△A′B′C′；然后利用正方形的面积减去周围多余三角形的面积可得△A′B′C′的面积．

解答 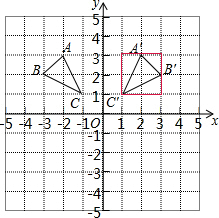解：如图所示：
△A′B′C′的面积：2×2-$\frac{1}{2}$×2×1-$\frac{1}{2}$×1×1-$\frac{1}{2}$×2×1=1.5．

点评 此题主要考查了作图--轴对称变换，关键是正确确定对称点的位置．

练习册系列答案
相关题目
16．已知：A-2B=7a2-7ab，且B=-3a2+6ab+4．
（1）求A等于多少？
（2）若|a+b-1|+（b-2）2=0，求A的值．
17．设一元二次方程x2-6x+3=0的两根为x1和x2，求$\frac{{x_2^{\;}}}{x_1}+\frac{x_1}{x_2}$的值．
14．已知（y2-1）x2+（y+1）x+4=0是关于x的一元一次方程，y=1．
1．在多项式x3-xy2+25中，常数项是（　　）
A．25B．x3，xy2C．x3，-xy2D．x3
11．探究题：
下图是某月的月历．

（1）如图1，带阴影的方框中的9个数之和是99；
（2）如果将带阴影的方框移至图2的位置，则这9个数之和是144；
（3）如果将带阴影的方框移至9个数之和为198的位置，求这9个数中最小的数．
18．在正方形ABCD中，AB=10cm，对角线AC、BD相交于O，则△ABO的周长是（　　）
A．10+5$\sqrt{2}$B．10+$\sqrt{2}$C．20+5$\sqrt{2}$D．10+10$\sqrt{2}$
15．下列计算正确的是（　　）
A．（x+y）（y-x）=x2-y2B．（-x+2y）2=x2-4xy+4y2
C．（2x-$\frac{1}{2}$y）2=4x2-xy+$\frac{1}{4}$y2D．（-3x-2y）2=9x2-12xy+4y2
16．当x=-2，分式$\frac{{{x^2}-2x-8}}{x-4}$的值为零．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网