题目内容
18.在正方形ABCD中,AB=10cm,对角线AC、BD相交于O,则△ABO的周长是( )| A. | 10+5$\sqrt{2}$ | B. | 10+$\sqrt{2}$ | C. | 20+5$\sqrt{2}$ | D. | 10+10$\sqrt{2}$ |
分析 由正方形的性质和勾股定理求出AC,得出OA、OB,即可得出△ABO的周长.
解答 解:在正方形ABCD中,AB=BC=10cm,
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10$\sqrt{2}$cm,
∴AO=BO=$\frac{1}{2}$AC=5$\sqrt{2}$cm,
则△AOB的周长=OA+OB+AB=5$\sqrt{2}$+5$\sqrt{2}$+10=10$\sqrt{2}$+10(cm).
故选:D.
点评 本题考查了正方形的性质、勾股定理、三角形周长的计算;熟练掌握正方形的性质,由勾股定理求出AC是解决问题的关键.

练习册系列答案
相关题目
13.国强同学喜欢用黑色棋子摆放在正多边形的边上来研究数的规律.请你观察下面表格中棋子的摆放规律,并回答下面问题:
(1)通过观察、归纳发现可以分别用含字母n(n≥1的整数)的代数式表示P、Q、M.则P=3n,Q=4n,M=n(n+2).
(2)下列数中既是三角形中的棋子数又是正方形中的棋子数的是D.
A.2013 B.2014 C.2015 D.2016.
三角形 |  | 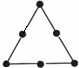 | 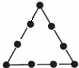 | … | 第n个 三角形 |
| 棋子个数 | 3 | 6 | 9 | … | P |
正方形 |  |  |  | … | 第n个 正方形 |
| 棋子个数 | 4 | 8 | 12 | … | Q |
正多边形 |  |  |  |  | 第n个 正多边形 |
| 棋子个数 | 3 | 8 | 15 | 24 | M |
(2)下列数中既是三角形中的棋子数又是正方形中的棋子数的是D.
A.2013 B.2014 C.2015 D.2016.
3.510表示的是( )
| A. | 5个10相乘 | B. | 10个5相乘 | C. | 5×10 | D. | 10个5相加 |
8. 如图,补充下列一个条件,不能使△ABD∽△ACB的是( )
如图,补充下列一个条件,不能使△ABD∽△ACB的是( )
 如图,补充下列一个条件,不能使△ABD∽△ACB的是( )
如图,补充下列一个条件,不能使△ABD∽△ACB的是( )| A. | ∠1=∠C | B. | ∠2=∠ABC | C. | $\frac{AD}{AB}=\frac{AB}{AC}$ | D. | $\frac{AD}{AB}=\frac{AB}{BC}$ |
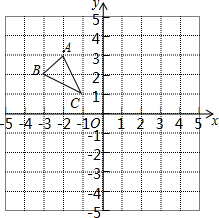 如图,在平面直角坐标系中,先画出△ABC关于y轴对称的△A′B′C′,并求出△A′B′C′的面积.
如图,在平面直角坐标系中,先画出△ABC关于y轴对称的△A′B′C′,并求出△A′B′C′的面积. 小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图.
小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图.