题目内容
17.设一元二次方程x2-6x+3=0的两根为x1和x2,求$\frac{{x_2^{\;}}}{x_1}+\frac{x_1}{x_2}$的值.分析 根据根与系数的关系得到x1+x2=6,x1x2=3,再利用通分和完全平方公式把$\frac{{x_2^{\;}}}{x_1}+\frac{x_1}{x_2}$变形为$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$,然后利用整体代入的方法计算.
解答 解:根据题意得x1+x2=6,x1x2=3,
所以$\frac{{x_2^{\;}}}{x_1}+\frac{x_1}{x_2}$=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{x}_{1}{x}_{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{{6}^{2}-2×3}{3}$=10.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
5.一元二次方程2x2+x-1=0的根的情况是( )
| A. | 有两个不等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
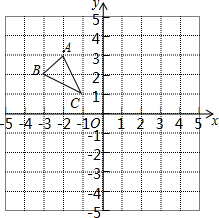 如图,在平面直角坐标系中,先画出△ABC关于y轴对称的△A′B′C′,并求出△A′B′C′的面积.
如图,在平面直角坐标系中,先画出△ABC关于y轴对称的△A′B′C′,并求出△A′B′C′的面积. 小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图.
小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图.