题目内容
操作发现
将一副直角三角板如图①摆放,能够发现等腰直角三角板ABC的斜边BC与30°角的直角三角板DEF的长直角边DE重合.
问题解决
将图①中的等腰三角板ABC绕点B顺时针旋转30°,点C落在BF上.AC与BD交于点O,连接CD,如图②.
(1)求证:△CDO是等腰三角形;
(2)若DF=2
,求AC的长.
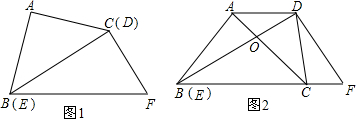
将一副直角三角板如图①摆放,能够发现等腰直角三角板ABC的斜边BC与30°角的直角三角板DEF的长直角边DE重合.
问题解决
将图①中的等腰三角板ABC绕点B顺时针旋转30°,点C落在BF上.AC与BD交于点O,连接CD,如图②.
(1)求证:△CDO是等腰三角形;
(2)若DF=2
| 3 |
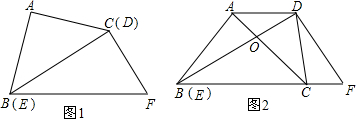
考点:旋转的性质,等腰三角形的判定与性质,解直角三角形
专题:
分析:(1)根据旋转的性质,可得BC与DE的关系,∠DBC的度数,根据三角形的外角的性质,可得∠DOC、∠OBC与∠OCB的关系,根据等腰三角形的判定,可得答案;
(2)根据正切的意义,可得BD的长,根据正弦的意义,可得答案.
(2)根据正切的意义,可得BD的长,根据正弦的意义,可得答案.
解答: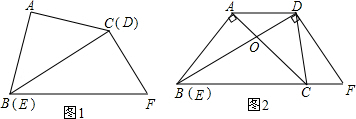
(1)证明:ABC绕点B顺时针旋转30°,
∴BC=DE,∠DEF=30°,
∴∠BDC=∠BCD.
∠BDC=∠BCD=(180°-∠DBC)÷2=75°.
∵∠ACB=45°,∠DOC=∠OBC+∠OCB,
∴∠DOC=30°+45°=75°.
∴∠COD=∠BDC.
∴△CDO是等腰三角形;
(2)在Rt△BDF中,DF=2
,
=tan∠DBF=tan30°=
,
∴BD=
•2
=6.
BC=BD=6
在Rt△ABC中,
=
=sin45°=
,
∴AC=
•6=3
.
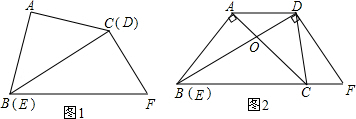
(1)证明:ABC绕点B顺时针旋转30°,
∴BC=DE,∠DEF=30°,
∴∠BDC=∠BCD.
∠BDC=∠BCD=(180°-∠DBC)÷2=75°.
∵∠ACB=45°,∠DOC=∠OBC+∠OCB,
∴∠DOC=30°+45°=75°.
∴∠COD=∠BDC.
∴△CDO是等腰三角形;
(2)在Rt△BDF中,DF=2
| 3 |
| DF |
| BD |
| ||
| 3 |
∴BD=
| 3 |
| 3 |
BC=BD=6
在Rt△ABC中,
| AC |
| BC |
| AC |
| 6 |
| ||
| 2 |
∴AC=
| ||
| 2 |
| 2 |
点评:本题考查了旋转的性质,(1)旋转前后的图形全等,三角形外角的性质,等腰三角形的判定;(2)锐角三角函数是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 对11月份本社接待的外地游客来杭州旅游的首选景点作了一次抽样调查. 调查结果如下图表:
对11月份本社接待的外地游客来杭州旅游的首选景点作了一次抽样调查. 调查结果如下图表: 如图,已知△ABC中,AB=AC,∠A=36°.
如图,已知△ABC中,AB=AC,∠A=36°.
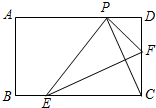 如图,在矩形纸片ABCD中,AB=3,BC=5,点E、F是BC、CD边上的动点(包括端点处),若将纸片沿EF折叠,使得点C恰好落在AD边上点P处.设CF=x,则x的取值范围为
如图,在矩形纸片ABCD中,AB=3,BC=5,点E、F是BC、CD边上的动点(包括端点处),若将纸片沿EF折叠,使得点C恰好落在AD边上点P处.设CF=x,则x的取值范围为