题目内容
已知,经过点A(-4,4)的抛物线y=ax2+bx+c与x轴相交于点B(-3,0)及原点O.
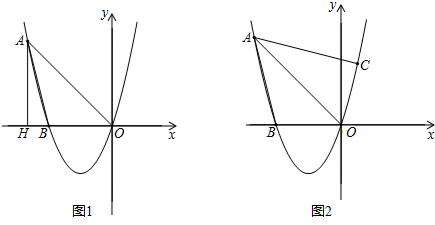
(1)求抛物线的解析式;
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,若点C在抛物线上,且∠CAO=∠BAO,试探究:在(2)的条件下,是否存在点G,使得△GOP∽△COA?若存在,请求出所有满足条件的点G坐标;若不存在,请说明理由.

(1)求抛物线的解析式;
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,若点C在抛物线上,且∠CAO=∠BAO,试探究:在(2)的条件下,是否存在点G,使得△GOP∽△COA?若存在,请求出所有满足条件的点G坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)根据已知点的坐标利用待定系数法确定二次函数的解析式即可;
(2)设点P坐标为(m,m2+3m),从而得到直线OA的解析式为y=-x,然后表示出点Q的坐标为(m,-m),进而表示出PQ=-m-(m2+3m)=-m2-4m,利用当四边形AHPQ为平行四边形时,PQ=AH=4得到-m2-4m=4,从而求得m的值,进而确定答案;
(3)设AC交y轴于点D,由点A(-4,4)得,∠AOB=∠AOD=45°,从而证得△AOD≌△AOB后表示点D坐标为(0,3),从而确定直线AC解析式,与二次函数联立即可得到点C的坐标,然后根据翻折的性质得到点G的坐标即可;
(2)设点P坐标为(m,m2+3m),从而得到直线OA的解析式为y=-x,然后表示出点Q的坐标为(m,-m),进而表示出PQ=-m-(m2+3m)=-m2-4m,利用当四边形AHPQ为平行四边形时,PQ=AH=4得到-m2-4m=4,从而求得m的值,进而确定答案;
(3)设AC交y轴于点D,由点A(-4,4)得,∠AOB=∠AOD=45°,从而证得△AOD≌△AOB后表示点D坐标为(0,3),从而确定直线AC解析式,与二次函数联立即可得到点C的坐标,然后根据翻折的性质得到点G的坐标即可;
解答:解:(1)由题意,得
,
解得
.
∴抛物线的解析式为y=x2+3x;
(2)设点P坐标为(m,m2+3m),其中-4<m<0
∵点A(-4,4),
∴直线OA的解析式为y=-x,
从而点Q的坐标为(m,-m)
∴PQ=-m-(m2+3m)=-m2-4m,
当四边形AHPQ为平行四边形时,PQ=AH=4,
即-m2-4m=4,解得m=-2(6分)
此时点P坐标为(-2,-2)
∴∠AOP=∠AOH+∠POH=45°+45°=90°.
(3)设AC交y轴于点D,由点A(-4,4)得,∠AOB=∠AOD=45°,
∵∠CAO=∠BAO,AO=AO,
∴△AOD≌△AOB,
∴OD=OB=3,点D坐标为(0,3),
设直线AC解析式为y=px+q,则
解得p=-
,q=3,∴直线AC解析式为y=-
x+3
解方程组
,得
,
(舍去),
∴点C坐标为(
,
).
将△AOC沿x轴翻折,得到△A1OC1,则A1(-4,-4),C1(
,-
)

∴O,P,A1都在直线y=x上,取OC1的中点G,则△GOP∽△C1OA1
∴△GOP∽△COA,此时点G坐标为(
,-
)(12分)
将△GOP沿直线y=x翻折,可得另一个满足条件的点G′(-
,
)
综上所述,点G的坐标为(
,-
)或(-
,
).
|
解得
|
∴抛物线的解析式为y=x2+3x;
(2)设点P坐标为(m,m2+3m),其中-4<m<0
∵点A(-4,4),
∴直线OA的解析式为y=-x,
从而点Q的坐标为(m,-m)
∴PQ=-m-(m2+3m)=-m2-4m,
当四边形AHPQ为平行四边形时,PQ=AH=4,
即-m2-4m=4,解得m=-2(6分)
此时点P坐标为(-2,-2)
∴∠AOP=∠AOH+∠POH=45°+45°=90°.
(3)设AC交y轴于点D,由点A(-4,4)得,∠AOB=∠AOD=45°,
∵∠CAO=∠BAO,AO=AO,
∴△AOD≌△AOB,
∴OD=OB=3,点D坐标为(0,3),
设直线AC解析式为y=px+q,则
|
解得p=-
| 1 |
| 4 |
| 1 |
| 4 |
解方程组
|
|
|
∴点C坐标为(
| 3 |
| 4 |
| 45 |
| 16 |
将△AOC沿x轴翻折,得到△A1OC1,则A1(-4,-4),C1(
| 3 |
| 4 |
| 45 |
| 16 |

∴O,P,A1都在直线y=x上,取OC1的中点G,则△GOP∽△C1OA1
∴△GOP∽△COA,此时点G坐标为(
| 3 |
| 8 |
| 45 |
| 32 |
将△GOP沿直线y=x翻折,可得另一个满足条件的点G′(-
| 45 |
| 32 |
| 3 |
| 8 |
综上所述,点G的坐标为(
| 3 |
| 8 |
| 45 |
| 32 |
| 45 |
| 32 |
| 3 |
| 8 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的解析式的求法.在求有关存在性的问题时要注意分析题意分情况讨论结果.

练习册系列答案
相关题目
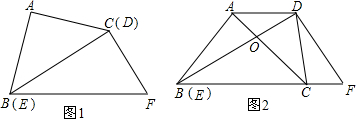
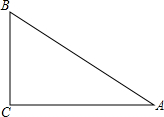 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.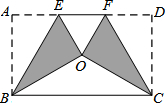 将矩形纸片ABCD按如图方式折叠,折痕是BE、CF,折叠后点A和点D重合在点O处,形成的△EOF是等边三角形,当
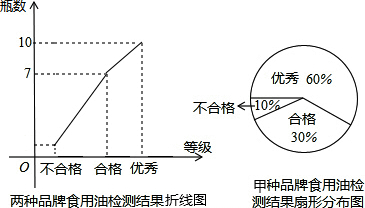
将矩形纸片ABCD按如图方式折叠,折痕是BE、CF,折叠后点A和点D重合在点O处,形成的△EOF是等边三角形,当 如图,用锤子以相同的力将铁钉垂直钉入木块,随着铁钉的深入,铁钉所受的阻力也越来越大.当铁钉进入木块部分长度足够时,每次钉入木块的铁钉长度是前一次的
如图,用锤子以相同的力将铁钉垂直钉入木块,随着铁钉的深入,铁钉所受的阻力也越来越大.当铁钉进入木块部分长度足够时,每次钉入木块的铁钉长度是前一次的