题目内容
如图，已知△ABC中，AB=AC，∠A=36°．（1）尺规作图：在AC上求作一点P，使BP+PC=AB．（保留作图痕迹，不写作法）
（2）在已作的图形中，连接PB，若AB=2cm，求底边BC的长．
考点：作图—相似变换,黄金分割
专题：
分析：（1）作∠ABC的角平分线BD，射线BD与AC的交点即所求的点P，进而得出答案；
（2）根据已知得出各角度数，进而求出△BPC∽△ABC，则
=
，即可得出答案．
（2）根据已知得出各角度数，进而求出△BPC∽△ABC，则
| BC |
| AB |
| PC |
| BC |
解答：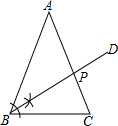
解：（1）作∠ABC的角平分线BD，射线BD与AC的交点即所求的点P，
如图射线BD即为所求；
（2）如图：∵AB=AC，∠A=36°，
∴∠ABC=∠C=72°，
∵∠ABP=∠CBP，
∴∠ABP=∠CBP=36°，
∴∠BPC=72°，
∴BC=BP，BP=AP，
∴AP=BP=BC，
∵∠A=∠CBP，∠C=∠C，
∴△BPC∽△ABC，
∴
=
，
=
，
解得：BC=-1+
或-1-
（负数舍去）．
解：（1）作∠ABC的角平分线BD，射线BD与AC的交点即所求的点P，如图射线BD即为所求；
（2）如图：∵AB=AC，∠A=36°，
∴∠ABC=∠C=72°，
∵∠ABP=∠CBP，
∴∠ABP=∠CBP=36°，
∴∠BPC=72°，
∴BC=BP，BP=AP，
∴AP=BP=BC，
∵∠A=∠CBP，∠C=∠C，
∴△BPC∽△ABC，
∴
| BC |
| AB |
| PC |
| BC |
| BC |
| 2 |
| 2-BC |
| BC |
解得：BC=-1+
| 5 |
| 5 |
点评：此题主要考查了复杂作图以及相似三角形的判定与性质等知识，得出AP=BP=BC是解题关键．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
（1）已知线段AB在平面内，在平面内找一点P使∠APB=90°．
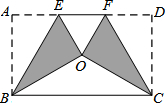将矩形纸片ABCD按如图方式折叠，折痕是BE、CF，折叠后点A和点D重合在点O处，形成的△EOF是等边三角形，当