题目内容
17．已知21-20=20，22-21=21，23-22=22…，则第n个等式为2n-2n-1=2n-1．分析 由已知等式知等式左右两边的幂的底数均为2，被减数的指数即为序数，减数和差的指数均比序数小1，据此可得．
解答 解：∵第1个等式为：21-20=20，
第2个等式为：22-21=21，
第3个等式为：23-22=22，
…
∴第n个等式为：2n-2n-1=2n-1，
故答案为：2n-2n-1=2n-1．
点评 本题主要考查数字的变化，根据已知等式得出左右两边的幂的底数均为2，被减数的指数即为序数，减数和差的指数均比序数小1是解题的关键．
练习册系列答案
相关题目
7．x=2时，px3+qx+1=2012，则x=-2时，代数式px3+qx+1的值为（ ）
| A． | 2011 | B． | -2012 | C． | -2010 | D． | 2013 |
8．某商场欲购进果汁饮料和碳酸饮料共150箱，两种饮料每箱的进价和售价如下表所示．设购进果汁饮料x箱（x为正整数），且所购进的两种饮料能全部卖出，获得的总利润为w元（注：总利润=总售价-总进价）．
（1）设购进碳酸饮料y箱，直接写出y与x的函数关系式为y=150-x；
（2）求总利润w关于x的函数关系式；
（3）如果购进两种饮料的总费用不超过7000元，那么该商场如何进货才能获利最多？并求出最大利润．
| 果汁饮料 | 碳酸饮料 | |
| 进价（元/箱） | 55 | 38 |
| 售价（元/箱） | 75 | 45 |
（2）求总利润w关于x的函数关系式；
（3）如果购进两种饮料的总费用不超过7000元，那么该商场如何进货才能获利最多？并求出最大利润．
将一副三角板如图放置，使点A在DE上，BC∥DE，则∠ACE的度数为15°．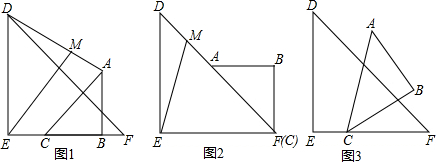
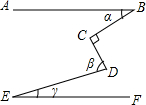如图，AB∥EF，∠C=90°，写出α、β、γ之间的等量关系是α+β-γ=90°．