题目内容
8. 如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,6),点D是OA的中点,点P在BC上运动,当△ODP是等腰三角形时,则P点的坐标为P1(2,6),P2(5,6),P3(8,6),P4(18,6).
如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,6),点D是OA的中点,点P在BC上运动,当△ODP是等腰三角形时,则P点的坐标为P1(2,6),P2(5,6),P3(8,6),P4(18,6).
分析 当P1O=OD=10或P2O=P2D或P3D=OD=10或P4D=OD=10时分别作P2E⊥OA于E,DF⊥BC于F,P4G⊥OA于G,利用勾股定理P1C,OE,P3F,DG的值,就可以求出P的坐标.
解答 解:当P1O=OD=10时,由勾股定理可以求得P1F=8,P1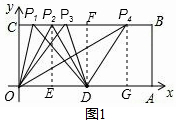 C=2,
C=2,
P2O=P2D时,作P2E⊥OA,
∴OE=ED=5;
当P3D=OD=10时,作DF⊥BC,由勾股定理,得P3F=2,
∴P3C=8;
当P4D=OD=10时,作P4G⊥OA,由勾股定理,得
DG=8,
∴OG=18.
∴P1(2,6),P2(5,6),P3(8,6),P4(18,6);
故答案为:P1(2,6),P2(5,6),P3(8,6),P4(18,6)
点评 本题考查了矩形的性质,关键是根据坐标与图形的性质,等腰三角形的性质和勾股定理的运用解答.

练习册系列答案
相关题目
20.某超市进了一批货,出售时要在进价的基础上加一定的利润,其销售量x(千克)与销售价c(元)之间的关系如下表:
(1)试用含有x的代数式表示售价c;
(2)若小华的妈妈想买8千克这种货物,那么她需要付多少钱?
(1)试用含有x的代数式表示售价c;
(2)若小华的妈妈想买8千克这种货物,那么她需要付多少钱?
| 销售量x(千克) | 销售价c(元) |
| 1 | 2+0.1 |
| 2 | 4+0.2 |
| 3 | 6+0.3 |
| 4 | 8+0.4 |
| … | … |
17.如果某个三角形的三个内角之比为1:2:1,那么这个三角形是( )
| A. | 等腰直角三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰三角形 |
 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.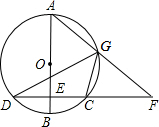 已知:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,G是弧AC上的任意一点,AG、DC的延长线相交于点F.
已知:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,G是弧AC上的任意一点,AG、DC的延长线相交于点F.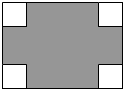 在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.
在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.