题目内容
13.在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为(2,4)或(-2,0)或(-2,4).(点C不与点A重合)分析 根据全等三角形的判定和已知点的坐标画出图形,即可得出答案.
解答 解:如图所示:
有三个点符合,
∵点A(2,0),B(0,4),
∴OB=4,OA=2,
∵△BOC与△AOB全等,
∴OB=OB=4,OA=OC=2,
∴C1(-2,0),C2(-2,4),C3(2,4).
故答案为:(2,4)或(-2,0)或(-2,4).
点评 本题考查了坐标与图形性质,全等三角形的判定与性质,难点在于根据点C的位置分情况讨论.

练习册系列答案
相关题目
1.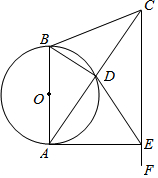 如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.
(1)试说明:△CBA∽△CDE;
(2)若AB=3,BD=2,求AE的长.
 如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.(1)试说明:△CBA∽△CDE;
(2)若AB=3,BD=2,求AE的长.
5.以下说法:
①两点确定一条直线;
②一条直线有且只有一条垂线;
③不相等的两个角一定不是对顶角;
④若|a|=-a,则a<0;
⑤若a,b互为相反数,则a,b的商必定等于-1.
其中正确的是①③.(请填序号)
①两点确定一条直线;
②一条直线有且只有一条垂线;
③不相等的两个角一定不是对顶角;
④若|a|=-a,则a<0;
⑤若a,b互为相反数,则a,b的商必定等于-1.
其中正确的是①③.(请填序号)
2.已知:4x=9y=6,则$\frac{1}{x}$+$\frac{1}{y}$等于( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
3.下面说法正确的是( )
| A. | 几个有理数相乘,当负因数有奇数个时积为负 | |
| B. | 近似数3.0万精确到千位 | |
| C. | 一个数的平方一定小于这个数 | |
| D. | 若|a|=-a,则a<0 |
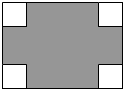 在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.
在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长. 将连续的奇数1,3,5,7,9…,排成如下的数表:
将连续的奇数1,3,5,7,9…,排成如下的数表: