题目内容
11.你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答过程会告诉你原因和方法.(1)阅读下列材料:
问题:利用一元一次方程将0.$\stackrel{•}{7}$化成分数.
解:设 0.$\stackrel{•}{7}$=x.
方程两边都乘以10,可得10×0.$\stackrel{•}{7}$=10x.
由0.$\stackrel{•}{7}$=0.777…,可知10×0.$\stackrel{•}{7}$=7.777…=7+0.$\stackrel{•}{7}$,
即 7+x=10x.(请你体会将方程两边都乘以10起到的作用)
可解得x=$\frac{7}{9}$,即0.$\stackrel{•}{7}$=$\frac{7}{9}$.
填空:将0.$\stackrel{•}{4}$写成分数形式为$\frac{4}{9}$.
(2)请你仿照上述方法把下列两个小数化成分数,要求写出利用一元一次方程进行解答的过程:①0.$\stackrel{•}{7}$$\stackrel{•}{3}$;②0.43$\stackrel{•}{2}$.
分析 (1)根据0.$\stackrel{•}{7}$转化分数的方法,设 0.$\stackrel{•}{4}$=x,仿照例题的解法即可得出结论;
(2)①根据0.$\stackrel{•}{7}$转化分数的方法,设0.$\stackrel{•}{7}$$\stackrel{•}{3}$=x,仿照例题的解法(×10换成×100)即可得出结论;
②根据0.$\stackrel{•}{7}$转化分数的方法,设0.43$\stackrel{•}{2}$=x,仿照例题的解法即可得出结论.
解答 解:(1)设0.$\stackrel{•}{4}$=x.
方程两边都乘以10,可得10×0.$\stackrel{•}{4}$=10x.
由0.$\stackrel{•}{4}$=0.444…,可知10×0.$\stackrel{•}{4}$=4.444…=4+0.$\stackrel{•}{4}$,
即4+x=10x.
解得:x=$\frac{4}{9}$,即0.$\stackrel{•}{4}$=$\frac{4}{9}$.
故答案为:$\frac{4}{9}$.
(2)①设0.$\stackrel{•}{7}$$\stackrel{•}{3}$=x.
方程两边都乘以100,可得100×0.$\stackrel{•}{7}$$\stackrel{•}{3}$=100x.
由0.$\stackrel{•}{7}$$\stackrel{•}{3}$=0.7373…,可知100×0.$\stackrel{•}{7}$$\stackrel{•}{3}$=73.7373…=73+0.$\stackrel{•}{7}$$\stackrel{•}{3}$,
即73+x=100x.
解得:x=$\frac{73}{99}$,即0.$\stackrel{•}{7}$$\stackrel{•}{3}$=$\frac{73}{99}$.
②设0.43$\stackrel{•}{2}$=x.
方程两边都乘以10,可得10×0.43$\stackrel{•}{2}$=10x.
由0.43$\stackrel{•}{2}$=0.43222…,可知10×0.43$\stackrel{•}{2}$=4.3222…=3.89+0.43$\stackrel{•}{2}$,
即3.89+x=10x.
解得:x=$\frac{389}{900}$,即0.43$\stackrel{•}{2}$=$\frac{389}{900}$.
点评 本题考查了一元一次方程的应用,读懂题意,能够仿照例题将循环小数转化为分数是解题的关键.

(1)试用含有x的代数式表示售价c;
(2)若小华的妈妈想买8千克这种货物,那么她需要付多少钱?
| 销售量x(千克) | 销售价c(元) |
| 1 | 2+0.1 |
| 2 | 4+0.2 |
| 3 | 6+0.3 |
| 4 | 8+0.4 |
| … | … |
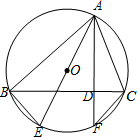 如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,弦AF与BC相交于点D,若BE=CF,求证:AF⊥BC.
如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,弦AF与BC相交于点D,若BE=CF,求证:AF⊥BC.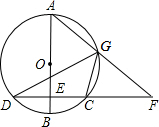 已知:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,G是弧AC上的任意一点,AG、DC的延长线相交于点F.
已知:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,G是弧AC上的任意一点,AG、DC的延长线相交于点F.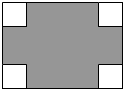 在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.
在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.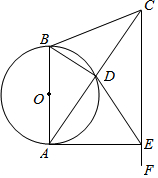 如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.