题目内容
18. 如图,在△ABC中,∠B=∠C,AB=10cm,BC=8cm,D为AB的中点,点P在线段上以3cm/s 的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动.当△BPD与△CQP全等时,求点P运动的时间.
如图,在△ABC中,∠B=∠C,AB=10cm,BC=8cm,D为AB的中点,点P在线段上以3cm/s 的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动.当△BPD与△CQP全等时,求点P运动的时间.
分析 根据等边对等角可得∠B=∠C,然后表示出BD、BP、PC、CQ,再根据全等三角形对应边相等,分①BD、PC是对应边,②BD与CQ是对应边两种情况讨论求解即可.
解答 解:∵AB=AC,
∴∠B=∠C,
设点P、Q的运动时间为t,则BP=3t,CQ=3t,
∵AB=10cm,BC=8cm,点D为AB的中点,
∴BD=$\frac{1}{2}$×10=5cm,
PC=(8-3t)cm,
①BD、PC是对应边时,∵△BPD与△CQP全等,
∴BD=PC,BP=CQ,
∴5=8-3t且3t=3t,
解得t=1,
②BD与CQ是对应边时,∵△BPD与△CQP全等,
∴BD=CQ,BP=PC,
∴5=3t,3t=8-3t,
解得t=$\frac{5}{3}$且t=$\frac{4}{3}$(舍去),
综上所述,△BPD与△CQP全等时,点P运动的时间为1秒.
点评 本题考查了全等三角形的对应边相等的性质,等边对等角的性质,根据对应角分情况讨论是本题的难点.

练习册系列答案
相关题目
9.若a、b为有理数,下列说法正确的是( )
| A. | 若a≠b,则a2≠b2 | B. | 若a2=b2,则a=b | ||
| C. | 若a>b,则a2>b2 | D. | 若a、b不全为零,则a2+b2>0 |
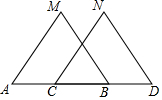 如图,已知MB=ND,∠MBA=∠NDC,如果∠M=∠N或∠A=∠NCD或AM∥CN或AB=CD,那么△ABM≌△CDN.
如图,已知MB=ND,∠MBA=∠NDC,如果∠M=∠N或∠A=∠NCD或AM∥CN或AB=CD,那么△ABM≌△CDN.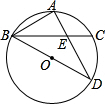 如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4
如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4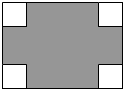 在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.
在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.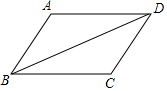 如图:请在下列四个条件:①AD∥BC,②AB=CD,③∠A=∠C,④AB∥CD中,选出两个,能推出△ABD≌△CDB:①②.(只要写出正确的一种即可)
如图:请在下列四个条件:①AD∥BC,②AB=CD,③∠A=∠C,④AB∥CD中,选出两个,能推出△ABD≌△CDB:①②.(只要写出正确的一种即可) 根据如图所示的计算程序,若输出的值为5,则输入的值为10或-2.
根据如图所示的计算程序,若输出的值为5,则输入的值为10或-2.