题目内容
15.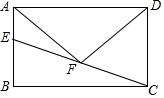 已知:如图,在矩形ABCD中,点E在边AB上,点F为CE的中点,连接AF、DF.
已知:如图,在矩形ABCD中,点E在边AB上,点F为CE的中点,连接AF、DF.(1)求证:△AFD为等腰三角形;
(2)若AB=3,AD=5,在不添加任何辅助线的情况下,请直接写出当△AFD的面积为整数时所有AE的长.
分析 (1)延长AF交DC延长线于点M,如图,先根据矩形的性质得到AB∥CD,∠ADC=90°,再利用平行线的性质得∠EAF=∠M,则可根据“ASA”判定△AFM≌△MFC,得到AF=FM,然后利用直角三角形斜边上的中线性质可判定△AFD为等腰三角形;
(2)设AE=x,△ADF的面积用S表示,利用全等的性质得到CM=AE=x,再根据三角形面积公式得到S△ADF=$\frac{1}{2}$S△ADM=$\frac{1}{2}$•$\frac{1}{2}$•5•(3+x),则x=$\frac{4S-15}{5}$,再利用0<x<3得到0<$\frac{4S-15}{5}$<3,解不等式得到得S的整数值为4、5、6、7,然后分别计算对应的x的值即可.
解答 (1)证明:延长AF交DC延长线于点M,如图,
∵四边形ABCD为ABCD,
∴AB∥CD,∠ADC=90°,
∴∠EAF=∠M,
在△AFM和△MFC中
$\left\{\begin{array}{l}{∠EAF=∠M}\\{FE=FC}\\{∠AFE=∠MFC}\end{array}\right.$,
∴△AFM≌△MFC,
∴AF=FM,
∴DF为Rt△ADM的斜边AM上的中线,
∴AF=DF=MF,
∴△AFD为等腰三角形;
(2)解:设AE=x,△ADF的面积用S表示,
∵△AFM≌△MFC,
∴CM=AE=x,
∵AF=MF,
∴S△ADF=$\frac{1}{2}$S△ADM=$\frac{1}{2}$•$\frac{1}{2}$•5•(3+x),
即S=$\frac{5x+15}{4}$,
∴x=$\frac{4S-15}{5}$,
∵0<x<3,
∴0<$\frac{4S-15}{5}$<3,解得3.75<S<7.5,
∴S的整数值为4、5、6、7,
当S=4时,x=$\frac{4S-15}{5}$=$\frac{1}{5}$,
当S=5时,x=$\frac{4S-15}{5}$=1,
当S=6时,x=$\frac{4S-15}{5}$=$\frac{9}{5}$,
当S=7时,x=$\frac{4S-15}{5}$=$\frac{13}{5}$,
即当△AFD的面积为整数时AE的长为$\frac{1}{5}$,1,$\frac{9}{5}$,$\frac{13}{5}$.
点评 本题考查了矩形的性质:平行四边形的性质矩形都具有;矩形的四个角都是直角.也考查了全等三角形的判定与性质.

(1)试用含有x的代数式表示售价c;
(2)若小华的妈妈想买8千克这种货物,那么她需要付多少钱?
| 销售量x(千克) | 销售价c(元) |
| 1 | 2+0.1 |
| 2 | 4+0.2 |
| 3 | 6+0.3 |
| 4 | 8+0.4 |
| … | … |
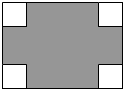 在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.
在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.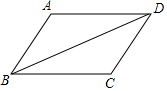 如图:请在下列四个条件:①AD∥BC,②AB=CD,③∠A=∠C,④AB∥CD中,选出两个,能推出△ABD≌△CDB:①②.(只要写出正确的一种即可)
如图:请在下列四个条件:①AD∥BC,②AB=CD,③∠A=∠C,④AB∥CD中,选出两个,能推出△ABD≌△CDB:①②.(只要写出正确的一种即可) 根据如图所示的计算程序,若输出的值为5,则输入的值为10或-2.
根据如图所示的计算程序,若输出的值为5,则输入的值为10或-2. 将连续的奇数1,3,5,7,9…,排成如下的数表:
将连续的奇数1,3,5,7,9…,排成如下的数表: