题目内容
16.甲、乙两人进行摸排游戏,现有三张形状大小完全相同的牌,正面分别标有数字2,3,5,将三张牌背面朝上,洗匀后放在桌子上.(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法写出所有可能的结果;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
分析 (1)根据题意直接列表,即可得出所有可能出现的结果;
(2)根据概率的意义分别求出甲、乙获胜的概率,再进行比较,即可得出答案.
解答 解:(1)所有可能出现的结果如图:
| 2 | 3 | 5 | |
| 2 | (2,2) | (2,3) | (2,5) |
| 3 | (3,2) | (3,3) | (3,5) |
| 5 | (5,2) | (5,3) | (5,5) |
(2)不公平.
从表格可以看出,两人抽取数字和为2的倍数有5种,两人抽取数字和为5的倍数有3种,所以甲获胜的概率为$\frac{5}{9}$,乙获胜的概率为$\frac{1}{3}$.
∵$\frac{5}{9}$>$\frac{1}{3}$,
∴甲获胜的概率大,游戏不公平.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
7. 如图,M、N、P、Q是数轴上的四个点,这四个点中最适合表示$\sqrt{15}$-1的点是( )
如图,M、N、P、Q是数轴上的四个点,这四个点中最适合表示$\sqrt{15}$-1的点是( )
 如图,M、N、P、Q是数轴上的四个点,这四个点中最适合表示$\sqrt{15}$-1的点是( )
如图,M、N、P、Q是数轴上的四个点,这四个点中最适合表示$\sqrt{15}$-1的点是( )| A. | 点M | B. | 点N | C. | 点P | D. | 点Q |
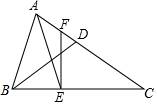 如图,△ABC中,D在AC边上,BD=CD,E在BC边上,AE=AB,过点E作EF⊥BC,交AC于F.若AD=5,CE=8,则EF的长为6.
如图,△ABC中,D在AC边上,BD=CD,E在BC边上,AE=AB,过点E作EF⊥BC,交AC于F.若AD=5,CE=8,则EF的长为6.
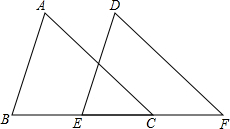 如图,点B,E,C,F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF,求证:AC∥DF.
如图,点B,E,C,F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF,求证:AC∥DF.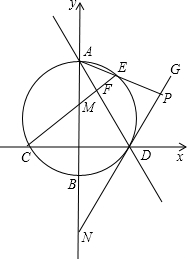 如图,点M在y轴的正半轴上,⊙M交x轴于C、D两点,交y轴于A、B两点,直线y=-2x+6经过A、D两点
如图,点M在y轴的正半轴上,⊙M交x轴于C、D两点,交y轴于A、B两点,直线y=-2x+6经过A、D两点 如图,已知A、B、C三点均在格点上,则tanA的值为$\frac{1}{2}$.
如图,已知A、B、C三点均在格点上,则tanA的值为$\frac{1}{2}$.