Question

6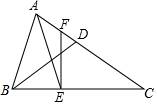．如图，△ABC中，D在AC边上，BD=CD，E在BC边上，AE=AB，过点E作EF⊥BC，交AC于F．若AD=5，CE=8，则EF的长为6．

Answer 1

分析 在AC上截取AG=BD，连接EG，作GM⊥BC于M．只要证明△ABD≌△EAG，推出AD=EG=5，由AG=BD=DC，推出AD=CG=GE=5，由GM⊥EC，推出EM=CM=4，在Rt△CMG中，GM=$\sqrt{{5}^{2}-{4}^{2}}$=3，由MG∥EF，EM=MC，推出FG=GC，可得GM=$\frac{1}{2}$EF，由此即可解决问题．

解答 解：在AC上截取AG=BD，连接EG，作GM⊥BC于M．
∵AE=AB，BD=CD，
∴∠C=∠DBC，∠ABE=∠ABE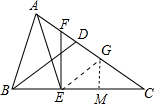
又∵∠AEB=∠C+∠EAC，∠ABE=∠CBD+∠DBA
∴∠ABD=∠EAC，
在△ABD和△EAG中，
$\left\{\begin{array}{l}{AB=AE}\\{∠BAE=∠EAG}\\{BD=AG}\end{array}\right.$，
∴△ABD≌△EAG
所以AD=EG=5，
∵AG=BD=DC，
∴AD=CG=GE=5，
∵GM⊥EC，
∴EM=CM=4，
在Rt△CMG中，GM=$\sqrt{{5}^{2}-{4}^{2}}$=3，
∵EF⊥BC，GM⊥BC，
∴MG∥EF，∵EM=MC，
∴FG=GC，
∴GM=$\frac{1}{2}$EF，
∴EF=6．
故答案为6．

点评 本题考查全等三角形的判定和性质、勾股定理、等腰三角形的性质、三角形的中位线定理，平行线等分线段定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，本题的突破点是证明GM是△EFC是中位线，属于中考填空题中的压轴题．