题目内容
12.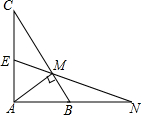 如图,△ABC中,∠BAC=90°,E为AC的中点,AM⊥BC于M,EM交AB的延长线于N.
如图,△ABC中,∠BAC=90°,E为AC的中点,AM⊥BC于M,EM交AB的延长线于N.(1)求证:AM2=BM•CM;
(2)若AM=2,EM=$\sqrt{5}$,求$\frac{BN}{MN}$.
分析 (1)证出∠AMB=∠CMA=90°,∠CAM=∠ABM,证明△CAM∽△ABM,得出的也不错了,即可得出结论;
(2)由直角三角形斜边上的中线性质得出AC=2EM=2$\sqrt{5}$,EM=CE,由勾股定理求出CM,得出BM,再证明△BMN∽△MAN,得出对应边成比例$\frac{BN}{MN}=\frac{BM}{AM}$,即可得出结果.
解答 (1)证明:∵∠BAC=90°,AM⊥BC,
∴∠BAM+∠CAM=90°,∠AMB=∠CMA=90°,
∴∠BAM+∠ABM=90°,
∴∠CAM=∠ABM,
∴△CAM∽△ABM,
∴AM:BM=CM:AM,
∴AM2=BM•CM;
(2)解:∵∠CMA=90°,E为AC的中点,
∴AC=2EM=2$\sqrt{5}$,EM=CE,
∴CM=$\sqrt{A{C}^{2}-A{M}^{2}}$=3$\sqrt{2}$,
∵AM2=BM•CM,
∴BM=$\frac{A{M}^{2}}{CM}$=$\frac{{2}^{2}}{3\sqrt{2}}$=$\frac{2\sqrt{2}}{3}$,
∵EM=CE,
∴∠C=∠EMC=∠BMN,
∵∠C=∠BAM,
∴∠BAM=∠BMN,
又∵∠N=∠N,
∴△BMN∽△MAN,
∴$\frac{BN}{MN}=\frac{BM}{AM}$=$\frac{\frac{2\sqrt{2}}{3}}{2}$=$\frac{\sqrt{2}}{3}$.
点评 本题考查了相似三角形的判定与性质、直角三角形斜边上的中线性质、勾股定理等知识;证明三角形相似得出对应边成比例是解决问题的关键.

练习册系列答案
相关题目
 如图,锐角△ABC中,∠ABC=45°,BD是∠ABC的平分线,BC=5,E为BC上一动点,F为BD上一动点,则CF+EF的最小值为$\frac{5\sqrt{2}}{2}$.
如图,锐角△ABC中,∠ABC=45°,BD是∠ABC的平分线,BC=5,E为BC上一动点,F为BD上一动点,则CF+EF的最小值为$\frac{5\sqrt{2}}{2}$.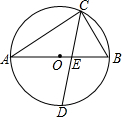 如图,AB为⊙O的直径,弦CD平分圆周角∠ACB,交AB于E,若AC=2BC,求$\frac{CE}{DE}$的值.
如图,AB为⊙O的直径,弦CD平分圆周角∠ACB,交AB于E,若AC=2BC,求$\frac{CE}{DE}$的值.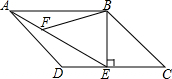 如图,已知在?ABCD中,过点B作BE⊥CD于点E,连接AE,F是AE上的点,且∠BFE=∠C.
如图,已知在?ABCD中,过点B作BE⊥CD于点E,连接AE,F是AE上的点,且∠BFE=∠C. 如图,Rt△ABO中,△AOB=90°,点A在第一象限、点B在第四象限,且AO:BO=1:$\sqrt{2}$,若已知点A在双曲线y=$\frac{1}{x}$上,点B在双曲线y=$\frac{k}{x}$上,求k的值.
如图,Rt△ABO中,△AOB=90°,点A在第一象限、点B在第四象限,且AO:BO=1:$\sqrt{2}$,若已知点A在双曲线y=$\frac{1}{x}$上,点B在双曲线y=$\frac{k}{x}$上,求k的值.