题目内容
4.已知△ABC的三边长BC=a,CA=b,AB=c,a,b,c都是整数,且a,b的最大公约数为2.点G和点I分别为△ABC的重心和内心,且∠GIC=90°.则△ABC的周长为35.分析 延长GI分别交BC于点P,AC于点Q,首先证明△CPQ为等腰三角形,根据内心和重心的知识分别表示出△PCQ的面积,进而求出a,b,c之间的等量关系式,最后对a,b,c进行讨论,进而求出a,b和c的值.
解答 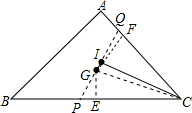 解:延长GI分别交BC于点P,AC于点Q,
解:延长GI分别交BC于点P,AC于点Q,
∵∠GIC=90°,
∴GI⊥CI,I是内心,
∴△CPQ为等腰三角形,
∴PC=QC,
∴S△PCQ=2S△CQI=r×CQ(r为三角形ABC内切圆半径)
∴S△PCQ=S△PGC+S△CGQ,
=$\frac{1}{2}$PC•ha(ha为GE⊥BC的高)+$\frac{1}{2}$CQ•hb(hb为GF⊥AC的高)
=$\frac{1}{2}$CQ(ha+hb)=r×CQ
∴2r=ha+hb①
∵r=$\frac{2{S}_{△ABC}}{a+b+c}$②
∵S△ABC=$\frac{1}{2}$×a•ha'(ha'为AM⊥BC的高)=$\frac{3}{2}$×a•ha,
∴ha=$\frac{2{S}_{△ABC}}{3a}$,hb=$\frac{2{S}_{△ABC}}{3b}$,
∴ha+hb=$\frac{2{S}_{△ABC}}{3a}$+$\frac{2{S}_{△ABC}}{3b}$③
把②③代入①得$\frac{6}{a+b+c}$,
当a=2,b=2时,c=2,
∵△ABC为等边三角形,
∴GI重合,舍去,
∴a≠b,
设a>b,a=2m,b=2n,
∵a、b的最大公约数为2,
∴(m,n)=1,
∴m+n整除12,
即m=7,n=5,
∴a=14,b=10,c=11,
∴a+b+c=35.
点评 本题考查了三角形的内切圆与内心:记住三角形内心的性质(三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角).解决本题的关键是求出∠DIF.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案| A. | y+3=2(2-y) | B. | 6y+3=2(2-y) | C. | 6y+3=4-y | D. | 6y+3=2-y |
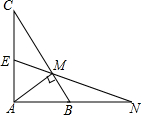 如图,△ABC中,∠BAC=90°,E为AC的中点,AM⊥BC于M,EM交AB的延长线于N.
如图,△ABC中,∠BAC=90°,E为AC的中点,AM⊥BC于M,EM交AB的延长线于N.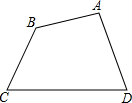 如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?
如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?