题目内容
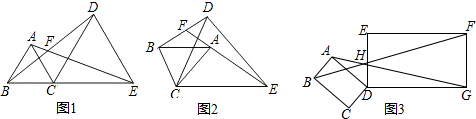
1.点B,C,E在同一直线上,点A,D在直线CE同侧,AB=AC,EC=ED,∠BAC=∠CED=70°,直线AE,BD交于点F.(1)如图(1),求证:△BCD∽△ACE,并求∠AFB的度数;
(2)如图(1)中的△ABC绕点C旋转一定角度,得图(2),求∠AFB的度数;
(3)拓展:如图(3),矩形ABCD和矩形DEFG中,AB=1,AD=ED=$\sqrt{3}$,DG=3,直线AG,BF交于点H,请直接写出∠AHB的度数.
分析 (1)由题意易得△ABC∽△EDC,进一步证得△BCD∽△ACE,进而可得∠AFB=∠CBD+∠AEC=∠CAE+∠AEC=∠ACB=55°,同理可得,∠AFB的大小;
(2)由题意易得△ABC∽△EDC,进一步证得△BCD∽△ACE,可求得∠AFB=∠BDC+∠CDE+∠DEF=∠CDE+∠CED,代入数据求大小;
(3)根据矩形的性质得到∠BAD=∠ADC=∠EDG=∠E=90°,根据勾股定理得到BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=2,DF=$\sqrt{D{E}^{2}+E{F}^{2}}$=2$\sqrt{3}$,根据三角函数的定义得到∠ADB=∠FDG=30°,推出△ADG∽△BDF,根据相似三角形的性质得到∠GAD=∠FBD,推出A,B,D,H四点共圆,根据圆周角定理即可得到结论.
解答 解:(1)∵AB=AC,EC=ED,∠BAC=∠CED=70°,
∴∠ACB=∠DCE=$\frac{1}{2}$(180°-70°)=55°,
∴△ABC∽△EDC,
∴$\frac{AC}{BC}=\frac{CD}{CE}$,
∵∠CBD=∠CAE,
∴△BCD∽△ACE;
∴∠AFB=180°-∠CAE-∠BAC-∠ABD,
=180°-∠BAC-∠ABC,
=∠ACB,
∴∠AFB=55°;
(2)∵AB=AC,EC=ED,∠BAC=∠CED,
∴∠ACB=∠DCE=$\frac{1}{2}$(180°-70°)=55°,
∴△ABC∽△EDC,
∴$\frac{BC}{CE}=\frac{AC}{CD}$,
∵∠BCD=∠ACE,
∴△BCD∽△ACE,
∴∠CBD=∠CAE,
∴∠BDC=∠AEC,
∴∠AFB=∠BDC+∠CDE+∠DEF,
=∠CDE+∠CED=180°-∠DCE,
∵AB=AC,EC=ED,∠BAC=∠DEC=70,
∴∠DCE=90°-$\frac{1}{2}$×70°=55°,
∴∠AFB=180°-55°=125°;
(3)连接BD,DF,
在矩形ABCD和矩形DEFG中,
∵∠BAD=∠ADC=∠EDG=∠E=90°,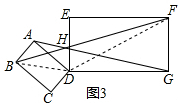
∵AB=1,AD=ED=$\sqrt{3}$,DG=3,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=2,DF=$\sqrt{D{E}^{2}+E{F}^{2}}$=2$\sqrt{3}$,
∴tan∠ADB=$\frac{AB}{AD}$=$\frac{\sqrt{3}}{3}$,tan∠FDG=$\frac{GF}{DG}$=$\frac{\sqrt{3}}{3}$,
∴∠ADB=∠FDG=30°,
∴$\frac{AD}{BD}=\frac{DG}{DF}=\frac{\sqrt{3}}{2}$,
∵∠ADG=90°+∠ADE,∠BDF=∠ADB+∠ADE+∠EDF=30°+∠ADE+90°-30°=90°+∠ADE,
∴∠ADG=∠BDF,
∴△ADG∽△BDF,
∴∠GAD=∠FBD,
∴A,B,D,H四点共圆,
∴∠AHB=∠ADB=30°.
点评 本题考查了相似三角形的判定与性质,等边三角形的性质,矩形的性质,勾股定理,解题时应根据图形旋转的变化规律,探究两个角之间的数量关系.并且本题突出考查从特殊与一般的数学思想和实验研究的能力,让学生经历了动手操作、观察猜想、合情推理、归纳证明等全过程,题目的难度不小.

 阅读快车系列答案
阅读快车系列答案 如图,要在河边修建一个水泵站,分别向A村、B村送水,已知:A、B到直线l的距离分别是1km和3km,两点的水平距离为3km,要在直线l上找到一个点P,使PA+PB得和最小,请在图中找出点P的位置,并计算PA+PB的最小值.
如图,要在河边修建一个水泵站,分别向A村、B村送水,已知:A、B到直线l的距离分别是1km和3km,两点的水平距离为3km,要在直线l上找到一个点P,使PA+PB得和最小,请在图中找出点P的位置,并计算PA+PB的最小值.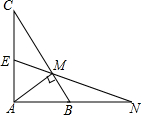 如图,△ABC中,∠BAC=90°,E为AC的中点,AM⊥BC于M,EM交AB的延长线于N.
如图,△ABC中,∠BAC=90°,E为AC的中点,AM⊥BC于M,EM交AB的延长线于N.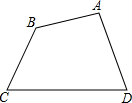 如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?
如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?