题目内容
7.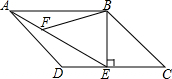 如图,已知在?ABCD中,过点B作BE⊥CD于点E,连接AE,F是AE上的点,且∠BFE=∠C.
如图,已知在?ABCD中,过点B作BE⊥CD于点E,连接AE,F是AE上的点,且∠BFE=∠C.(1)求证:△ABF∽△EAD;
(2)若AB=4,CE=2,AE=5,求AF的长.
分析 (1)根据平行四边形的性质得出AB∥CD,AD∥BC,求出∠BAF=∠AED,∠AFB=∠D,根据相似三角形的判定得出即可;
(2)根据相似得出$\frac{AB}{AE}$=$\frac{AF}{DE}$,代入求出即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠BAF=∠AED,∠C+∠D=180°,
∵∠BFE=∠C,∠BFE+∠AFB=180°,
∴∠AFB=∠D,
∵∠BAF=∠AED,
∴△ABF∽△EAD;
(2)解:∵四边形ABCD是平行四边形,AB=4,
∴DC=AB=4,
∵CE=2,
∴DE=4-2=2,
∵△ABF∽△EAD,
∴$\frac{AB}{AE}$=$\frac{AF}{DE}$,
∴$\frac{4}{5}$=$\frac{AF}{2}$,
解得:AF=1.6.
点评 本题考查了平行四边形的性质,平行线的性质,相似三角形的性质和判定的应用,能求出△ABF∽△EAD是解此题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
18.按某种标准把多项式分类,4x2-4与a3b+2ab2属于同一类,则下列多项式中也属于这一类的是( )
| A. | -x5+y3 | B. | 3x3+x+1 | C. | 2ab+cd+2 | D. | a4+3a3+2ab2+b3 |
17.抛物线y=-x2+2x-3的对称轴是直线( )
| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
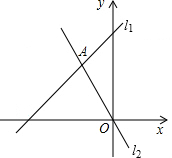 如图,直线l1:y=kx+b与l2:y=-2x相交于A(-2,4),那么不等式kx+b>-2x的解集为x>-2.
如图,直线l1:y=kx+b与l2:y=-2x相交于A(-2,4),那么不等式kx+b>-2x的解集为x>-2.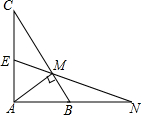 如图,△ABC中,∠BAC=90°,E为AC的中点,AM⊥BC于M,EM交AB的延长线于N.
如图,△ABC中,∠BAC=90°,E为AC的中点,AM⊥BC于M,EM交AB的延长线于N.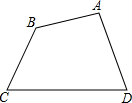 如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?
如图,四边形ABCD,某图形设计要求把该四边形改设计成一个平行四边形且面积扩大为原来的2倍,A、B、C、D这四点必须在新的平行四边形的四条边上.你能给出一种符合要求的设计方案吗?