��Ŀ����
16��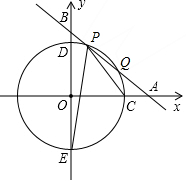 ��ͼ��ƽ��ֱ������ϵxOy�У�һ�κ���y=-x+b��bΪ������b��0����ͼ����x�ᡢy��ֱ���A��B���㣬�뾶Ϊ5��Բ��O��x���������ཻ�ڵ�C����y���ཻ��D��E���㣮
��ͼ��ƽ��ֱ������ϵxOy�У�һ�κ���y=-x+b��bΪ������b��0����ͼ����x�ᡢy��ֱ���A��B���㣬�뾶Ϊ5��Բ��O��x���������ཻ�ڵ�C����y���ཻ��D��E���㣮��1����ֱ��AB���ӻ�$\widehat{CD}$��P��Q���㣨����C��D��
�ٵ�P������Ϊ��3��4��ʱ����bֵ��
�����CPE�Ķ��������ú�b�Ĵ���ʽ��ʾ��PQ�ij���д��b��ȡֵ��Χ����
��2����b=6ʱ���߶�AB�ϴ��ڼ�����F��ʹ��CFE=45�㣿��˵�����ɣ�
���� ��1����ֱ�ӽ���P���������ֱ��y=-x+b�У��������b��ֵ��
�������ֱ��OM�Ľ���ʽ�����ɵó���M�����꣬�����ó�OM�����ù��ɶ������ɵó�PM�����ɵó�PQ��
��2�����жϳ���F���ӻ�$\widehat{CD}$��ʱ����CFE=45�㣬�����ж�b=6���߶�AB���O�Ľ���ĸ������ɵó����ۣ�
��� �⣺��1���١ߵ�P��3��4����ֱ��AB�ϣ�
��-3+b=4��
��b=7��
�ڡߡ�COE=90�㣬
���CPE=$\frac{1}{2}$��COE=45�㣬
��ͼ1�� ����O��OM��AB��M������OP��
����O��OM��AB��M������OP��
��ֱ��AB�Ľ���ʽΪy=-x+b�٣�
��ֱ��OM�Ľ���ʽΪy=x�ڣ�
�����٢ڽ�õ�M��$\frac{1}{2}$b��$\frac{1}{2}$b����
��OM2=$\frac{1}{2}$b2��
��Rt��POM�У�OP=5�����ݹ��ɶ����ã�PM=$\sqrt{O{P}^{2}-O{M}^{2}}$=$\frac{\sqrt{2}}{2}$$\sqrt{50-{b}^{2}}$��
��PQ=2PM=$\sqrt{2}$•$\sqrt{50-{b}^{2}}$��
����P�͵�D�غ�ʱ��b=5
��OM=5ʱ��b=-5$\sqrt{2}$���ᣩ��b=5$\sqrt{2}$��
��5��b��5$\sqrt{2}$��
����PQ=$\sqrt{2}$•$\sqrt{50-{b}^{2}}$��5��b��5$\sqrt{2}$����
��2����b=6ʱ���߶�AB�ϴ���2����F��ʹ��CFE=45�㣬
���ɣ��ɣ�1����֪����F���ӻ�$\widehat{CD}$��ʱ����CFE=45�㣬
�ɣ�1����֪��OM=5ʱ������b=5$\sqrt{2}$ʱ��ֱ��AB���O���У�
����B���D�غ�ʱ��b=5��
�൱b=6ʱ����5��5$\sqrt{2}$֮�䣬
���߶�AB���Q���������㣬
������b=6ʱ���߶�AB�ϴ���2����F��ʹ��CFE=45�㣮
���� ������һ�κ����ۺ��⣬��Ҫ�����˴���ϵ����ȷ��ֱ�ߵĽ���ʽ�����ɶ�����ֱ�ߺ�Բ��λ�ù�ϵ���⣨1���ٵĹؼ������ô���ϵ������ֱ��OM�Ľ���ʽ���⣨1���ڵĹؼ��ǹ���ֱ�������Σ��⣨3���Ĺؼ����ж�b=6ʱ���߶�AB��ԲO�Ľ��������

��1���Զ�����ȣ�
��2��ȫ�������ε������ȣ�
��3���߶δ�ֱƽ�����ϵĵ㵽�����߶������˵�ľ�����ȣ�
��4�����x��0����ôx2��0��
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
| A�� | -8ab | B�� | -4ab | C�� | 8ab | D�� | 4ab |
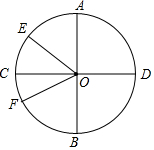 ��ͼ��ԲO��ֱ��Ϊ10cm������ֱ��AB��CD�ཻ��90��ǣ���AOE=50�㣬OF�ǡ�BOE��ƽ���ߣ�
��ͼ��ԲO��ֱ��Ϊ10cm������ֱ��AB��CD�ཻ��90��ǣ���AOE=50�㣬OF�ǡ�BOE��ƽ���ߣ�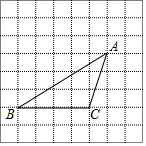 ��ͼ��������ֽ�е�������ABC������ƽ��2��õ�������DEF���ٽ�������DEF����ƽ��3��õ�������GPH��
��ͼ��������ֽ�е�������ABC������ƽ��2��õ�������DEF���ٽ�������DEF����ƽ��3��õ�������GPH��