题目内容
7.已知a,b满足$\sqrt{4a-5b}$+$\sqrt{a-b-1}$=0,则$\sqrt{ab}$÷$\sqrt{\frac{{b}^{3}}{a}}$-b=-$\frac{11}{4}$.分析 利用非负数的性质列出方程组,求出方程组的解得到a与b的值,代入原式计算即可得到结果.
解答 解:∵$\sqrt{4a-5b}$+$\sqrt{a-b-1}$=0,
∴$\left\{\begin{array}{l}{4a-5b=0}\\{a-b-1=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=5}\\{b=4}\end{array}\right.$,
则原式=2$\sqrt{5}$÷$\frac{8\sqrt{5}}{5}$-4=-$\frac{11}{4}$,
故答案为:-$\frac{11}{4}$
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
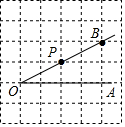 点P是∠AOB的边OB上一点.
点P是∠AOB的边OB上一点.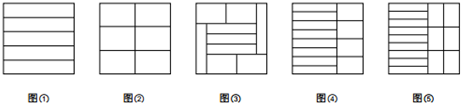
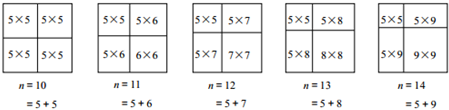
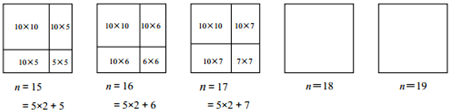
 (一)阅读
(一)阅读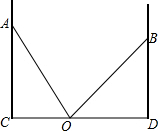 如图,已知AC、BD为数值的墙面,一架梯子从点O竖起,当靠在墙面AC上时,梯子的另一端落在点A处,此时∠AOC=60°,当靠在墙面BD上时,梯子的另一端落在点B处,此时∠BOD=45°,且OD=3$\sqrt{2}$米.
如图,已知AC、BD为数值的墙面,一架梯子从点O竖起,当靠在墙面AC上时,梯子的另一端落在点A处,此时∠AOC=60°,当靠在墙面BD上时,梯子的另一端落在点B处,此时∠BOD=45°,且OD=3$\sqrt{2}$米.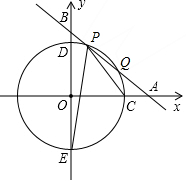 如图,平面直角坐标系xOy中,一次函数y=-x+b(b为常数,b>0)的图象与x轴、y轴分别交于A、B两点,半径为5的圆⊙O与x轴正半轴相交于点C,与y轴相交于D、E两点.
如图,平面直角坐标系xOy中,一次函数y=-x+b(b为常数,b>0)的图象与x轴、y轴分别交于A、B两点,半径为5的圆⊙O与x轴正半轴相交于点C,与y轴相交于D、E两点.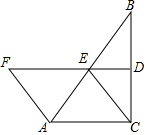 如图,∠ACB=90°,D,E分别为BC,AB的中点,DE的延长线交AF于F,∠F=∠FEA.
如图,∠ACB=90°,D,E分别为BC,AB的中点,DE的延长线交AF于F,∠F=∠FEA.