题目内容
6.下列命题的逆命题是真命题的有( )(1)对顶角相等;
(2)全等三角形的面积相等;
(3)线段垂直平分线上的点到这条线段两个端点的距离相等;
(4)如果x>0,那么x2>0.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 分别写出各个命题的逆命题,然后判断正误即可.
解答 解:(1)对顶角相等的逆命题为相等的角为对顶角,错误,是假命题;
(2)全等三角形的面积相等的逆命题为面积相等的三角形全等,错误,是假命题;
(3)线段垂直平分线上的点到这条线段两个端点的距离相等的逆命题为到线段两端点距离相等的点在线段的垂直平分线上,正确,是真命题;
(4)如果x>0,那么x2>0的逆命题为如果x2>0,那么x>0,故错误,是假命题,
故选A.
点评 本题考查了命题与定理的知识,解题的关键是能够正确的写出各个命题的逆命题并正确的进行判断,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列图形不可由平移得到的是( )
| A. |  | B. |  | C. |  | D. |  |
1.下列各式中与-2xy-x2-y2的相等的是( )
| A. | (x+y)2 | B. | -(x+y)2 | C. | (x-y)2 | D. | -(x-y)2 |
 如图所示,AB⊥l1,AC⊥l2,则点A到直线l1的距离是线段AB的长度.
如图所示,AB⊥l1,AC⊥l2,则点A到直线l1的距离是线段AB的长度.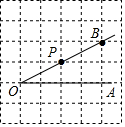 点P是∠AOB的边OB上一点.
点P是∠AOB的边OB上一点. 如图,Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿AD折叠,使AC落在斜边AB上且与AE重合,则CD=3.
如图,Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿AD折叠,使AC落在斜边AB上且与AE重合,则CD=3.
 (一)阅读
(一)阅读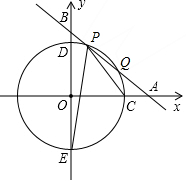 如图,平面直角坐标系xOy中,一次函数y=-x+b(b为常数,b>0)的图象与x轴、y轴分别交于A、B两点,半径为5的圆⊙O与x轴正半轴相交于点C,与y轴相交于D、E两点.
如图,平面直角坐标系xOy中,一次函数y=-x+b(b为常数,b>0)的图象与x轴、y轴分别交于A、B两点,半径为5的圆⊙O与x轴正半轴相交于点C,与y轴相交于D、E两点.