题目内容
10.已知△ABC,若有|sinA-$\frac{1}{2}}$|与(tanB-$\sqrt{3}$)2互为相反数,则∠C的度数是90°.分析 直接利用特殊角的三角函数值以及绝对值以及偶次方的性质得出∠A,∠B的度数进而得出答案.
解答 解:∵|sinA-$\frac{1}{2}}$|与(tanB-$\sqrt{3}$)2互为相反数,
∴sinA-$\frac{1}{2}$=0,tanB-$\sqrt{3}$=0,
则sinA=$\frac{1}{2}$,tanB=$\sqrt{3}$,
∴∠A=30°,∠B=60°,
则∠C的度数是:90°.
故答案为:90°.
点评 此题主要考查了特殊角的三角函数值以及绝对值以及偶次方的性质等知识,正确应用绝对值以及偶次方的性质是解题关键.

练习册系列答案
相关题目
1.下列命题中正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 菱形的周长等于两条对角线长之和的两倍 | |
| C. | 对角线相等的平行四边形是菱形 | |
| D. | 菱形的面积等于两条对角线长之积的一半 |
18.若$\sqrt{x-1}+\sqrt{x+y}=0$,则x2015+y2016的值( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
5.某工厂要建一个面积为130m2的仓库,仓库的一边靠墙(墙长为16m),并在与墙平行的一边开一道1m宽的门,现有能围成32m的木板,求仓库的长与宽?若设垂直于墙的边长为x米,则列出的方程为( )
| A. | x•(32-2x+1)=130 | B. | $\frac{{({32-2x+1})}}{2}•x=130$ | C. | x•(32-2x-1)=130 | D. | $\frac{{({32-2x-1})}}{2}•x=130$ |
19.若二次根式$\sqrt{x+1}$有意义,则x的可取的数是( )
| A. | 比1小的数 | B. | 不小于-1的数 | C. | 不大于-1的数 | D. | 全体实数 |
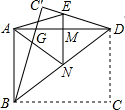 如图,一张宽为3,长为4的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于M,则ME=$\frac{7}{12}$.
如图,一张宽为3,长为4的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于M,则ME=$\frac{7}{12}$.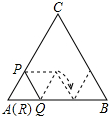 如图,正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为2π cm.(结果保留π)
如图,正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为2π cm.(结果保留π)