Question

5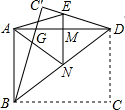．如图，一张宽为3，长为4的矩形纸片ABCD，先沿对角线BD对折，点C落在C′的位置，BC′交AD于G，再折叠一次，使点D与点A重合，得折痕EN，EN交AD于M，则ME=$\frac{7}{12}$．

Answer 1

分析 由折叠的性质与矩形的性质，证得△BGD是等腰三角形，则在Rt△ABG中，利用勾股定理，借助于方程即可求得AG的长，又由△ABG≌△C′DG，得到∠EDM=∠ABG，由三角函数的性质即可求得ME的长．

解答 解：根据折叠的性质可得：∠GBD=∠CBD，AM=DM=$\frac{1}{2}$AD，∠EMA=∠EMD=90°，
∵四边形ABCD是矩形，
∴AD∥BC，AD=BC=4，∠BAD=90°，
∴∠ADB=∠CBD，
∴∠GBD=∠ADB，
∴BG=DG，
设AG=x，则BG=DG=4-x，
∵在Rt△ABG中，AB²+AG²=BG²，
∴3²+x²=（4-x）²，
∴x=$\frac{7}{8}$，
即AG=$\frac{7}{8}$，
在△AGB和△C′GD中，
$\left\{\begin{array}{l}{∠BAG=∠DC′G}\\{∠AGB=∠C′GD}\\{AB=C′D}\end{array}\right.$，
∴△AGB≌△C′GD，
∴∠EDM=∠ABG，
∴$\frac{EM}{MD}$=$\frac{AG}{AB}$=$\frac{7}{24}$，又MD=2，
∴EM=$\frac{7}{12}$，
故答案为：$\frac{7}{12}$．

点评 此题考查了折叠的性质，全等三角形的判定与性质，三角函数的性质以及勾股定理等知识．此题综合性较强，解题时要注意数形结合思想与方程思想的应用．