题目内容
15.若两个最简二次根式$\sqrt{2a}$与$\sqrt{9-a}$可以合并,则a=3.分析 由于两个最简二次根式可以合并,因此它们是同类二次根式,即被开方数相同.由此可列出一个关于a的方程,解方程即可求出a的值.
解答 解:由题意得,2a=9-a,
解得a=3.
故答案为:3.
点评 此题主要考查了同类二次根式的定义,即:化成最简二次根式后,被开方数相同,这样的二次根式叫做同类二次根式.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
3.若方程组$\left\{{\begin{array}{l}{ax+by=3}\\{2ax+by=4}\end{array}}\right.$与方程组$\left\{{\begin{array}{l}{2x+y=3}\\{x-y=0}\end{array}}\right.$有相同的解,则a、b的值分别为( )
| A. | 1,2 | B. | 1,0 | C. | $\frac{1}{3},-\frac{2}{3}$ | D. | $-\frac{1}{3},\frac{2}{3}$ |
4. 如图,在△ABC中,∠C=90°,AC=18,BC=20,若有一半径为9的圆分别与AC和BC相切,则下列可找到此圆圆心的方法是( )
如图,在△ABC中,∠C=90°,AC=18,BC=20,若有一半径为9的圆分别与AC和BC相切,则下列可找到此圆圆心的方法是( )
 如图,在△ABC中,∠C=90°,AC=18,BC=20,若有一半径为9的圆分别与AC和BC相切,则下列可找到此圆圆心的方法是( )
如图,在△ABC中,∠C=90°,AC=18,BC=20,若有一半径为9的圆分别与AC和BC相切,则下列可找到此圆圆心的方法是( )| A. | BC的垂直平分线与AC的垂直平分线的交点 | |
| B. | ∠C的平分线与BC的垂直平分线的交点 | |
| C. | ∠C的平分线与AC的垂直平分线的交点 | |
| D. | ∠C的平分线与AB的垂直平分线的交点 |
5.三角形中,到三边距离相等的点是( )
| A. | 三条角平分线的交点 | B. | 三边垂直平分线的交点 | ||
| C. | 三条高线的交点 | D. | 三条中线的交点 |
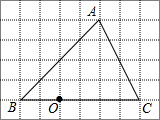 如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.
如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.