题目内容
18.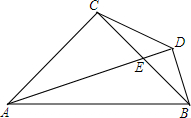 知图,△ACB为等腰直角三角形,∠ACB=90°,AC=BC,AE平分∠BAC,BD⊥AE,垂足为D点.
知图,△ACB为等腰直角三角形,∠ACB=90°,AC=BC,AE平分∠BAC,BD⊥AE,垂足为D点.(1)求证:AE=2BD;
(2)求∠ADC的度数.
分析 (1)延长AC和BD相交于点F,由直角三角形的性质得出∠AEC=∠F,由AAS证明△ACE≌△BCF,得出对应边相等AE=BF,证出∠F=∠ABD,得出AB=AF,由等腰三角形的三线合一性质得出BD=FD=$\frac{1}{2}$BF=$\frac{1}{2}$AE,即可得出结论;
(2)由等腰直角三角形的性质得出∠ABC=45°,证出A、B、D、C四点共圆,由圆周角定理得出∠ADC=∠ABC=45°即可.
解答 (1)证明:延长AC和BD相交于点F,如图所示: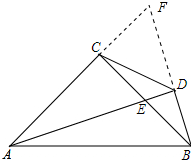
则∠BCF=180°-∠ACB=90°,
∵BD⊥AE于D,
∴∠ADF=∠ADB=90°,
∴∠F+∠CAE=90°,
∵∠AEC+∠CAE=90°,
∴∠AEC=∠F,
在△ACE和△BCF中,
$\left\{\begin{array}{l}{∠ACE=∠BCF=90°}&{\;}\\{∠AEC=∠F}&{\;}\\{AC=BC}&{\;}\end{array}\right.$,
∴△ACE≌△BCF(AAS),
∴AE=BF,
∵AE平分∠BAC,
∴∠CAE=∠BAE,
∵∠F+∠CAE=90°,∠ABD+∠BAE=90°,
∴∠F=∠ABD,
∴AB=AF,
∵BD⊥AE于D,
∴BD=FD=$\frac{1}{2}$BF=$\frac{1}{2}$AE,
∴AE=2BD;
(2)解:∵∠ACB=∠ADB=90°,AC=BC,
∴∠ABC=45°,A、B、D、C四点共圆,
∴∠ADC=∠ABC=45°.
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、等腰直角三角形的性质、四点共圆、圆周角定理等知识;本题综合性强,有一定难度,需要通过作辅助线证明三角形全等和四点共圆才能得出结论.

练习册系列答案
相关题目
20.已知抛物线y=x2-2mx+m2+m+2与x轴的交点为(a,0),(b,0),则(a-1)2+(b-1)2的最小值是( )
| A. | 10 | B. | 15 | C. | 18 | D. | 20 |
 把两个含有45°角的直角三角板如图放置,点D在BC点上,连接BE、AD,AD的延长线交BE于点F,则∠AFB=90°.
把两个含有45°角的直角三角板如图放置,点D在BC点上,连接BE、AD,AD的延长线交BE于点F,则∠AFB=90°.
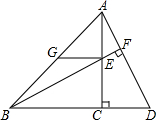 已知,如图,在等腰Rt△ABC中,∠ACB=90°,点D、E分别在BC延长线及AC上,联结BE并延长交AD于F,过点E作EG∥BC交AB于G,AC=EG+CD.求证:BF⊥AD.
已知,如图,在等腰Rt△ABC中,∠ACB=90°,点D、E分别在BC延长线及AC上,联结BE并延长交AD于F,过点E作EG∥BC交AB于G,AC=EG+CD.求证:BF⊥AD.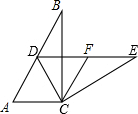 如图,在Rt△ABC中,∠ACB=90°,∠B=α,将△ABC绕点C按顺时针方向旋转β后得到△DEC,点D恰好落在AB边上.
如图,在Rt△ABC中,∠ACB=90°,∠B=α,将△ABC绕点C按顺时针方向旋转β后得到△DEC,点D恰好落在AB边上.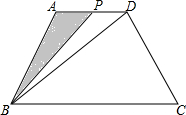 四边形ABCD中,AD∥BC,AB=CD=5,AD=7,BC=13,S四边形ABCD=40,P是一动点,沿AD,DC由A经D点向C点移动,设P点移动的距离为x.
四边形ABCD中,AD∥BC,AB=CD=5,AD=7,BC=13,S四边形ABCD=40,P是一动点,沿AD,DC由A经D点向C点移动,设P点移动的距离为x.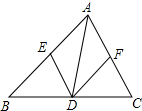 如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.求证:AE=DF.
如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.求证:AE=DF.