题目内容
10.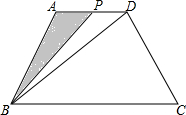 四边形ABCD中,AD∥BC,AB=CD=5,AD=7,BC=13,S四边形ABCD=40,P是一动点,沿AD,DC由A经D点向C点移动,设P点移动的距离为x.
四边形ABCD中,AD∥BC,AB=CD=5,AD=7,BC=13,S四边形ABCD=40,P是一动点,沿AD,DC由A经D点向C点移动,设P点移动的距离为x.(1)当P点在AD上运动时,求△PAB的面积y与x的函数关系式并画出图象;
(2)当P点继续沿DC向C点运动时,求四边形ADPB的面积y与x的函数关系式.
分析 (1)作AE垂直BC于E,根据梯形的面积公式得到函数的解析式;
(2)根据勾股定理得到BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=3.根据等腰梯形的性质得到∠ABE=∠C;AD=BC-2BE=7.作PF垂直BC于F.由∠ABE=∠C,∠AEB=∠PFC=90°.得到△AEB∽△PFC,根据相似三角形的性质得到$\frac{AE}{PF}=\frac{AB}{PC}$,代入数据求得PF=$\frac{48-4x}{5}$,根据图形的面积公式即可得到结论.
解答 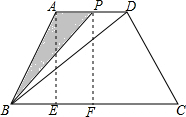 解:(1)作AE垂直BC于E,
解:(1)作AE垂直BC于E,
∵AD=7,BC=13,S四边形ABCD=40,
∴$\frac{1}{2}$(AD+BC)•AE=40,AE=4,
∴y=$\frac{1}{2}$AAP•AE=$\frac{1}{2}•x•4$=2x;
(2)∵BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=3,
∵AB=CD=5,∴梯形ABCD为等腰梯形,
∴∠ABE=∠C;AD=BC-2BE=7,
∵AD+DP=x,PD=x-7; PC=CD-PD=5-(x-7)=12-x,
作PF垂直BC于F.
∵∠ABE=∠C;∠AEB=∠PFC=90°.
∴△AEB∽△PFC,
∴$\frac{AE}{PF}=\frac{AB}{PC}$,
即:$\frac{4}{PF}=\frac{5}{12-x}$,
∴PF=$\frac{48-4x}{5}$,
∵S梯形ABCD=$\frac{1}{2}$(AD+BC)•AE=$\frac{1}{2}$(7+13)×4=40,
S△BCP=$\frac{1}{2}$BC•PF=$\frac{1}{2}×13×\frac{48-4x}{5}$=$\frac{312-26x}{5}$,
∴y=S梯形ABCD-S△BCP=40-$\frac{312-26x}{5}$,
即:y=$\frac{26}{5}$x-$\frac{112}{5}$.(7≤x≤12).
点评 本题考查了动点问题的函数图象,等腰梯形的性质,图形的面积计算,根据图形的面积公式求函数的解析式,正确的识图是解题的关键.

 如图,长方形ABCD的边与坐标轴平行,点A、C的坐标分别为(-1,1),($\sqrt{3}$,-2$\sqrt{3}$)
如图,长方形ABCD的边与坐标轴平行,点A、C的坐标分别为(-1,1),($\sqrt{3}$,-2$\sqrt{3}$) 知图,△ACB为等腰直角三角形,∠ACB=90°,AC=BC,AE平分∠BAC,BD⊥AE,垂足为D点.
知图,△ACB为等腰直角三角形,∠ACB=90°,AC=BC,AE平分∠BAC,BD⊥AE,垂足为D点.
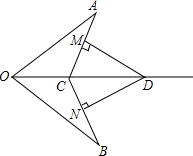 如图,已知C,D在∠AOB的平分线上,OA=OB,DM⊥AC于点M,DN⊥BC于点N.求证:DM=DN.
如图,已知C,D在∠AOB的平分线上,OA=OB,DM⊥AC于点M,DN⊥BC于点N.求证:DM=DN. 阅读理解
阅读理解