题目内容
13.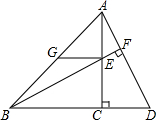 已知,如图,在等腰Rt△ABC中,∠ACB=90°,点D、E分别在BC延长线及AC上,联结BE并延长交AD于F,过点E作EG∥BC交AB于G,AC=EG+CD.求证:BF⊥AD.
已知,如图,在等腰Rt△ABC中,∠ACB=90°,点D、E分别在BC延长线及AC上,联结BE并延长交AD于F,过点E作EG∥BC交AB于G,AC=EG+CD.求证:BF⊥AD.
分析 根据EG∥BC得出△AEG是等腰直角三角形,利用AC=EG+CD得出EC=CD,利用SAS证明△BCE≌△ACD,利用全等三角形的性质证明即可.
解答 证明:∵EG∥BC,且∠ACB=90°,等腰Rt△ABC,
∴∠AEG=90°,∠AGE=∠ABC=45°,
∴AE=GE,
∵AC=EG+CD,AC=AE+EC,
∴EC=CD,
在△BCE与△ACD中,
$\left\{\begin{array}{l}{EC=CD}\\{∠ECB=∠ACD=90°}\\{BC=AC}\end{array}\right.$,
∴△BCE≌△ACD(SAS),
∴∠EBC=∠CAD,
∵∠ACD+∠D=90°,
∴∠EBC+∠D=90°,
∴∠BFD=90°,
∴BF⊥AD.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(SSS、SAS、ASA、AAS和HL)和性质(全等三角形的对应边、对应角相等)是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
14.若关于x的分式方程$\frac{m}{x-1}$-$\frac{2}{1-x}$=1的解为正数,则m的取值范围是( )
| A. | m>-3 | B. | m≠1 | C. | m>-3且m≠-2 | D. | m>-3且m≠1 |
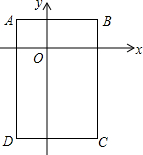 如图,长方形ABCD的边与坐标轴平行,点A、C的坐标分别为(-1,1),($\sqrt{3}$,-2$\sqrt{3}$)
如图,长方形ABCD的边与坐标轴平行,点A、C的坐标分别为(-1,1),($\sqrt{3}$,-2$\sqrt{3}$) 如图,正方形ABCD中,E、F两点分别在BC、CD上,BE+DF=EF.求证:
如图,正方形ABCD中,E、F两点分别在BC、CD上,BE+DF=EF.求证: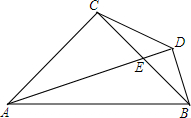 知图,△ACB为等腰直角三角形,∠ACB=90°,AC=BC,AE平分∠BAC,BD⊥AE,垂足为D点.
知图,△ACB为等腰直角三角形,∠ACB=90°,AC=BC,AE平分∠BAC,BD⊥AE,垂足为D点.