题目内容
利民商店经销甲、乙两种商品.现有如下信息:
信息1:按零售单价购买甲商品3件和乙商品2件,共付了19元.商品的进货单价之和是5元;
信息2:甲商品零售单价比进货单价多1元,乙商品零售单价比进货单价的2倍少1元.
信息3:按零售单价购买甲商品3件和乙商品2件
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进货单价各多少元?
(2)该商店平均每天卖出甲商品500件和乙商品300件.经调查发现,甲、乙两种商品零售单价分别每降0.1元,这两种商品每天可各多销售100件.为了使每天获取更大的利润,商店决定把甲、乙两种商品的零售单价都下降m元.在不考虑其他因素的条件下,当m定为多少时,才能使商店每天销售甲、乙两种商品获取的利润最大?每天的最大利润是多少?
信息1:按零售单价购买甲商品3件和乙商品2件,共付了19元.商品的进货单价之和是5元;
信息2:甲商品零售单价比进货单价多1元,乙商品零售单价比进货单价的2倍少1元.
信息3:按零售单价购买甲商品3件和乙商品2件
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进货单价各多少元?
(2)该商店平均每天卖出甲商品500件和乙商品300件.经调查发现,甲、乙两种商品零售单价分别每降0.1元,这两种商品每天可各多销售100件.为了使每天获取更大的利润,商店决定把甲、乙两种商品的零售单价都下降m元.在不考虑其他因素的条件下,当m定为多少时,才能使商店每天销售甲、乙两种商品获取的利润最大?每天的最大利润是多少?
考点:二次函数的应用,二元一次方程组的应用
专题:
分析:(1)根据题意,列出方程组求解,即可解决问题.
(2)根据题意列出关于m的函数关系式,借助二次函数的性质即可解决问题.
(2)根据题意列出关于m的函数关系式,借助二次函数的性质即可解决问题.
解答:解:(1)设甲商品的进货单价是x元,乙商品的进货单价是y元.
由题意得
解得
答:甲商品的进货单价是2元,乙商品的进货单价是3元.
(2)由题意知甲种商品每件获取的利润为1元,乙种商品每件获取的
利润为2元,设商店每天销售甲、乙两种商品获取的利润为s元,
则s=(1-m)(500+100×
)+(2-m)(300+100×
)
即 s=-2000m2+2200m+1100=-2000(m-0.55)2+1705.
∵-2000<0
∴当m=0.55时,s有最大值,最大值为1705.
答:当m定为0.55元时,才能使商店每天销售甲、乙两种商品获取的利润最大,每天的最大利润是1705元.
由题意得
|
解得
|
答:甲商品的进货单价是2元,乙商品的进货单价是3元.
(2)由题意知甲种商品每件获取的利润为1元,乙种商品每件获取的
利润为2元,设商店每天销售甲、乙两种商品获取的利润为s元,
则s=(1-m)(500+100×
| m |
| 0.1 |
| m |
| 0.1 |
即 s=-2000m2+2200m+1100=-2000(m-0.55)2+1705.
∵-2000<0
∴当m=0.55时,s有最大值,最大值为1705.
答:当m定为0.55元时,才能使商店每天销售甲、乙两种商品获取的利润最大,每天的最大利润是1705元.
点评:该题以二次函数为载体,以二元一次方程组的应用、二次函数的性质及其应用为考查的核心构造而成;解题的关键是深入把握题意,准确找出命题中隐含的数量关系;灵活运用有关性质来分析、判断、解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
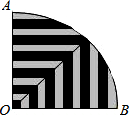 将如图所示的圆心角为90°的扇形条纹纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(接缝粘贴部分忽略不计),OA=OB=8,则围成的圆锥形纸帽的高是
将如图所示的圆心角为90°的扇形条纹纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(接缝粘贴部分忽略不计),OA=OB=8,则围成的圆锥形纸帽的高是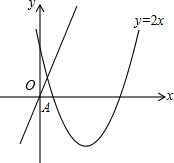 已知抛物线y=2x2+bx+6经过A(1,0),点P为抛物线的顶点,点B为抛物线与x轴的另一交点.
已知抛物线y=2x2+bx+6经过A(1,0),点P为抛物线的顶点,点B为抛物线与x轴的另一交点. 如图,数轴上线段AB的中点表示的数是
如图,数轴上线段AB的中点表示的数是 如图,已知BO,CO分别是∠ABC的外角平分线,试说明∠BOC=90°-
如图,已知BO,CO分别是∠ABC的外角平分线,试说明∠BOC=90°-