题目内容
6.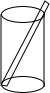 一种乘饮料的圆柱形杯子,测得内部底面半径为2.5cm,高为12cm,吸管最放进杯里(如图),杯口外面露出部分的吸管长为4.6cm,问吸管为多长?
一种乘饮料的圆柱形杯子,测得内部底面半径为2.5cm,高为12cm,吸管最放进杯里(如图),杯口外面露出部分的吸管长为4.6cm,问吸管为多长?
分析 根据筷子、杯子的直径及高恰好构成直角三角形,求出AB的长,再由勾股定理即可得出结论.
解答 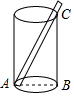 解:∵杯子底面半径为2.5cm,高为12cm,
解:∵杯子底面半径为2.5cm,高为12cm,
∴AB=2×2.5=5cm,BC=12cm,
∵吸管、圆柱形杯内部底面直径与杯壁正好构成直角三角形,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13cm,
∵杯口外面露出4.6cm,
∴吸管的长为:13+4.6=17.6cm.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时,勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
16. 如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
 如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
1. 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )
 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )| A. | -3<x<2 | B. | -3<x<0或x>2 | C. | x>-3 | D. | x<2 |
11.计算:-3+10=( )
| A. | -13 | B. | 7 | C. | -30 | D. | -7 |
18.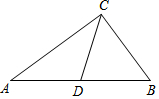 已知Rt△ABC中,∠ACB=90°,∠B=54°,CD是斜边AB上的中线,则∠ACD的度数是( )
已知Rt△ABC中,∠ACB=90°,∠B=54°,CD是斜边AB上的中线,则∠ACD的度数是( )
 已知Rt△ABC中,∠ACB=90°,∠B=54°,CD是斜边AB上的中线,则∠ACD的度数是( )
已知Rt△ABC中,∠ACB=90°,∠B=54°,CD是斜边AB上的中线,则∠ACD的度数是( )| A. | 18° | B. | 36° | C. | 54° | D. | 72° |
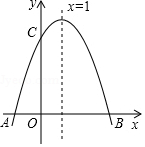 如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,交y轴于C点,其中B点坐标为(3,0),C点坐标为(0,3),且图象对称轴为直线x=1.
如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,交y轴于C点,其中B点坐标为(3,0),C点坐标为(0,3),且图象对称轴为直线x=1.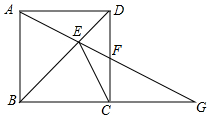 如图,ABCD是正方形,G是BC延长线上一点,AG交BD于E,交CD于F,求证:CE与△CFG的外接圆相切.
如图,ABCD是正方形,G是BC延长线上一点,AG交BD于E,交CD于F,求证:CE与△CFG的外接圆相切.