题目内容
16．
如图，在△ABC中，AD、BE是两条中线，则S△ABP：S△EDP=（ ）| A． | 1：2 | B． | 1：3 | C． | 1：4 | D． | 2：3 |
分析 根据三角形的中位线得出DE∥AB，DE=$\frac{1}{2}$AB，根据平行线的性质得出相似，根据相似三角形的性质求出即可．
解答 解：∵AD、BE是两条中线，
∴DE=$\frac{1}{2}$AB，DE∥AB，
∴$\frac{DE}{AB}$=$\frac{1}{2}$，△ABP∽△EDP，
∴S△ABP：S△EDP=4：1，
故选：C．
点评 本题考查了相似三角形的性质和判定，三角形的中位线的应用，注意：相似三角形的面积比等于相似比的平方，三角形的中位线平行于第三边，并且等于第三边的一半．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知△ABC，∠ABC，∠ACB的角平分线交于点O，连接AO并延长交BC于D，OH⊥BC于H，若∠BAC=60°，OH=3cm，OA长为（ ）cm．
4．如果∠1的补角是∠2，且∠1＞∠2，那么∠2是（ ）
| A． | 直角 | B． | 锐角 | C． | 钝角 | D． | 平角 |
8．下列方程中是一元一次方程的是（ ）
| A． | 4x-5=0 | B． | 2x-y=3 | C． | 3x2-14=2 | D． | $\frac{1}{x}$-2=3 |
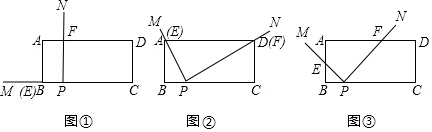
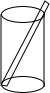一种乘饮料的圆柱形杯子，测得内部底面半径为2.5cm，高为12cm，吸管最放进杯里（如图），杯口外面露出部分的吸管长为4.6cm，问吸管为多长？