题目内容
12.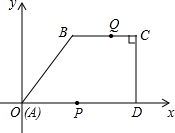 如图所示,在四边形ABCD中,AD∥CB,∠C=90°,D,B两点坐标分别为D(15,0),B(5,12),动点P,Q分别从O,C两点出发,点P以每秒2个单位的速度沿AD向终点D运动,点Q以每秒1个单位的速度沿CB向点B运动,当点P停止运动时,点Q也同时停止运动,设动点P,Q运动的时间为t(单位:秒)
如图所示,在四边形ABCD中,AD∥CB,∠C=90°,D,B两点坐标分别为D(15,0),B(5,12),动点P,Q分别从O,C两点出发,点P以每秒2个单位的速度沿AD向终点D运动,点Q以每秒1个单位的速度沿CB向点B运动,当点P停止运动时,点Q也同时停止运动,设动点P,Q运动的时间为t(单位:秒)(1)当t为何值时,四边形PABQ是平行四边形;
(2)当t为何值时,四边形PABQ是梯形且两腰AB=PQ?
分析 (1)当BQ=AP时,四边形PABQ是平行四边形,由题意得:QC=t个单位/秒,AP=2t个单位/秒,然后可得方程10-t=2t,再解即可;
(2)过B作BE⊥AD,过Q作QF⊥AD,先证明Rt△ABE≌Rt△PQF可得AE=FP,然后可得方程10-t=2t-5-5,再解即可.
解答 解:(1)当BQ=AP时,四边形PABQ是平行四边形,
由题意得:QC=t个单位/秒,AP=2t个单位/秒,
∵B(5,12),D(15,0),
∴C(15,12),
∴BC=10,
∴10-t=2t,
解得:t=$\frac{10}{3}$;
(2)过B作BE⊥AD,过Q作QF⊥AD,
∵BE⊥AD,QF⊥AD,
∴∠BEA=∠QFP=90°,
∵BC∥AD,
∴EB=QF,
在Rt△ABE和Rt△PQF中,
$\left\{\begin{array}{l}{BE=QF}\\{AB=QP}\end{array}\right.$,
∴Rt△ABE≌Rt△PQF(HL),
∴AE=FP,
∵B(5,12),
∴PF=5,
t秒后AP=2t,QB=10-t,
∴10-t=2t-5-5,
解得:t=$\frac{20}{3}$.
点评 此题主要考查了平行四边形的判定和动点问题,关键是掌握一组对边平行且相等的四边形是平行四边形.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
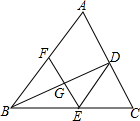 如图,BD是△ABC的平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.
如图,BD是△ABC的平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.
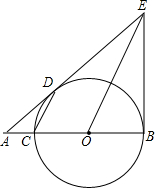 已知如图,BC是圆O直径,BE是圆O的切线,切点为B,OE平行于弦CD,ED,BC的延长线交于点A,若AC=1,且AC,AD的长是关于x的方程x2-mx+2=0的两个根
已知如图,BC是圆O直径,BE是圆O的切线,切点为B,OE平行于弦CD,ED,BC的延长线交于点A,若AC=1,且AC,AD的长是关于x的方程x2-mx+2=0的两个根