题目内容
4.有两条平行直线m、n、AOB是两平行线的一折线,则我们会有这样的结论:∠O=∠1+∠2.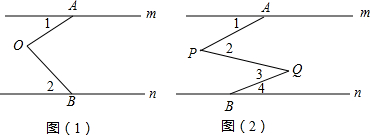
(1)证明该结论;
(2)如果将折一次改为折两次如图(2)∠1,∠2,∠3,∠4会满足怎样的关系,证明你的结论;
(3)若此折线继续折下去,折三次,折四次…折n次,又会得到怎样的结论?请你用自己的语言来描述所得到的结论(不必证明).
分析 (1)过O作l∥m,根据平行线性质推出∠1=∠3,∠2=∠4,相加即可求出答案;
(2)过Q作QM∥m,PN∥m,根据平行线性质求出∠1=∠APN,∠NPQ=∠MQP,∠MQB=∠4,代入求出即可;
(3)根据(1)、(2)总结出规律.
解答 (1)证明:过O作l∥m,如图(1),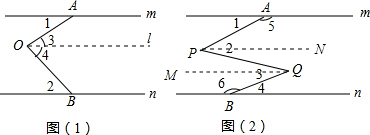
∵m∥n,
∴m∥l∥n,
∴∠1=∠3,∠4=∠2,
∴∠1+∠2=∠3+∠4,
即∠AOB=∠1+∠2;
(2)∠1,∠2,∠3,∠4会满足的关系式是:∠1+∠3=∠2+∠4,
解:过O作QM∥m,PN∥m,如图(2)
∵m∥n,
∴m∥QM∥PN∥n,
∴∠1=∠APN,∠NPQ=∠MQP,∠MQB=∠4,
∴∠1+∠PQM+∠MQB=∠APN+∠NPQ+∠4,
即:∠1+∠3=∠2+∠4;
(3)如果两平行线间存在折线,则所有同向角的和相等.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.解此题的关键是正确作辅助线,并根据证出的结果得出规律,题目比较典型,但是有一定的难度.

练习册系列答案
相关题目
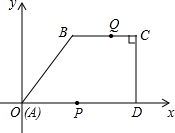 如图所示,在四边形ABCD中,AD∥CB,∠C=90°,D,B两点坐标分别为D(15,0),B(5,12),动点P,Q分别从O,C两点出发,点P以每秒2个单位的速度沿AD向终点D运动,点Q以每秒1个单位的速度沿CB向点B运动,当点P停止运动时,点Q也同时停止运动,设动点P,Q运动的时间为t(单位:秒)
如图所示,在四边形ABCD中,AD∥CB,∠C=90°,D,B两点坐标分别为D(15,0),B(5,12),动点P,Q分别从O,C两点出发,点P以每秒2个单位的速度沿AD向终点D运动,点Q以每秒1个单位的速度沿CB向点B运动,当点P停止运动时,点Q也同时停止运动,设动点P,Q运动的时间为t(单位:秒) 如图,在梯形ABCD中,AD∥BC,E是AB的中点,EF⊥CD于点F,求证:S梯形ABCD=EF•CD.
如图,在梯形ABCD中,AD∥BC,E是AB的中点,EF⊥CD于点F,求证:S梯形ABCD=EF•CD.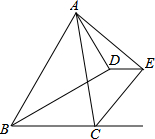 在△ABC中,BD平分∠ABC,CE平分∠ACB的外角,AD⊥BD,AE⊥CE,若DE=$\frac{3}{2}$,AE=$\frac{7}{2}$,∠ABC=60°,则AB=5.
在△ABC中,BD平分∠ABC,CE平分∠ACB的外角,AD⊥BD,AE⊥CE,若DE=$\frac{3}{2}$,AE=$\frac{7}{2}$,∠ABC=60°,则AB=5.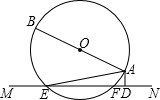 如图:AB是⊙O的直径,直线MN与⊙O相交于点E、F,AD⊥MN,垂足为D.
如图:AB是⊙O的直径,直线MN与⊙O相交于点E、F,AD⊥MN,垂足为D.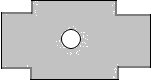 某校在教学楼前铺设小广场地面,其图案设计如图所示.若长方形地面的长为50米,宽为32米,中心建一直径为10米的圆形喷泉,四周各角留一个长20米,宽5米的小长方形花坛,图中阴影处铺设广场地砖.求阴影部分的面积S(π取3).
某校在教学楼前铺设小广场地面,其图案设计如图所示.若长方形地面的长为50米,宽为32米,中心建一直径为10米的圆形喷泉,四周各角留一个长20米,宽5米的小长方形花坛,图中阴影处铺设广场地砖.求阴影部分的面积S(π取3).