题目内容
16.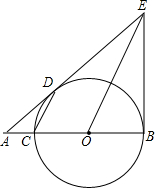 已知如图,BC是圆O直径,BE是圆O的切线,切点为B,OE平行于弦CD,ED,BC的延长线交于点A,若AC=1,且AC,AD的长是关于x的方程x2-mx+2=0的两个根
已知如图,BC是圆O直径,BE是圆O的切线,切点为B,OE平行于弦CD,ED,BC的延长线交于点A,若AC=1,且AC,AD的长是关于x的方程x2-mx+2=0的两个根(1)证明:AE是圆O的切线;
(2)求线段BE的长;
(3)求tan∠ADC的值.
分析 (1)如图由BC是⊙O直径,BE是⊙O的切线,得到∠EBO=90°根据平行线和等腰三角形的性质,得到∠1=∠4,通过全等三角形证得.
(2)根据一元二次方程的根与系数的关系,求得AD的长,由切割线定理求出AB的长,根据勾股定理列方程求得;
(3)由切割线定理求得AB的长,得到圆的直径,然后在Rt△ABE中,根据勾股定理求出BE的长,则RECOD中,即可求得∠OED的正切值,由于∠ADC=∠OED,由此可求出∠ADC的正切值.
解答 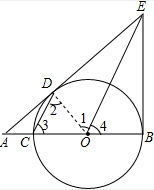 解:(1)证明:如图,
解:(1)证明:如图,
∵BC是⊙O直径,BE是⊙O的切线,
∴∠EBO=90°,
∵OE∥CD,
∴∠1=∠2,∠3=∠4,
∵OD=OC,
∴∠2=∠3,
∴∠1=∠4,
在△DOE与△BOE中,
$\left\{\begin{array}{l}{OD=OB}\\{∠1=∠4}\\{OE=OE}\end{array}\right.$,
∴△DOE≌△BOE(SAS),
∴∠ODE=∠B=90°,
∴AE⊥OD,
∴AE是⊙O的切线;
(2)∵AC,AD的长是关于X的方程x2-mx+2=0的两个根,AC=1,
∴AD=2,
由切割线定理得:AD2=AC•AB,
∴AB=4,
由(1)证得△DOE≌△BOE,
∴BE=DE,
∴BE2+42=(2+BE)2,
∴BE=3;
(3)∵AB=4,AC=1,
∴BC=3,
∵CD∥OE,
∴∠ADC=∠AEO,
∴tan∠ADC=tan∠AEO=$\frac{OD}{DE}$=$\frac{\frac{3}{2}}{3}$=$\frac{1}{2}$.
点评 本题主要考查了切线的性质、平行线的判定、全等三角形的判定和性质以及勾股定理等知识,关键是(3)要找到∠ADC的等角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
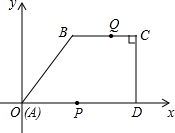 如图所示,在四边形ABCD中,AD∥CB,∠C=90°,D,B两点坐标分别为D(15,0),B(5,12),动点P,Q分别从O,C两点出发,点P以每秒2个单位的速度沿AD向终点D运动,点Q以每秒1个单位的速度沿CB向点B运动,当点P停止运动时,点Q也同时停止运动,设动点P,Q运动的时间为t(单位:秒)
如图所示,在四边形ABCD中,AD∥CB,∠C=90°,D,B两点坐标分别为D(15,0),B(5,12),动点P,Q分别从O,C两点出发,点P以每秒2个单位的速度沿AD向终点D运动,点Q以每秒1个单位的速度沿CB向点B运动,当点P停止运动时,点Q也同时停止运动,设动点P,Q运动的时间为t(单位:秒)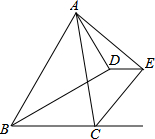 在△ABC中,BD平分∠ABC,CE平分∠ACB的外角,AD⊥BD,AE⊥CE,若DE=$\frac{3}{2}$,AE=$\frac{7}{2}$,∠ABC=60°,则AB=5.
在△ABC中,BD平分∠ABC,CE平分∠ACB的外角,AD⊥BD,AE⊥CE,若DE=$\frac{3}{2}$,AE=$\frac{7}{2}$,∠ABC=60°,则AB=5.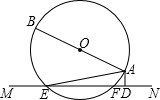 如图:AB是⊙O的直径,直线MN与⊙O相交于点E、F,AD⊥MN,垂足为D.
如图:AB是⊙O的直径,直线MN与⊙O相交于点E、F,AD⊥MN,垂足为D.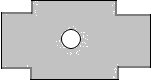 某校在教学楼前铺设小广场地面,其图案设计如图所示.若长方形地面的长为50米,宽为32米,中心建一直径为10米的圆形喷泉,四周各角留一个长20米,宽5米的小长方形花坛,图中阴影处铺设广场地砖.求阴影部分的面积S(π取3).
某校在教学楼前铺设小广场地面,其图案设计如图所示.若长方形地面的长为50米,宽为32米,中心建一直径为10米的圆形喷泉,四周各角留一个长20米,宽5米的小长方形花坛,图中阴影处铺设广场地砖.求阴影部分的面积S(π取3).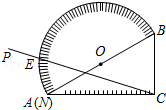 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第15秒,点E在量角器上对应的读数是90度.
如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第15秒,点E在量角器上对应的读数是90度.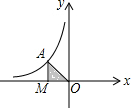 如图,点A是反比例函数在第二象限的图象上任一点,AM⊥x轴于M,O是原点,如果△AOM的面积是2,则该反比例函数的解析式为y=$\frac{-4}{x}$.
如图,点A是反比例函数在第二象限的图象上任一点,AM⊥x轴于M,O是原点,如果△AOM的面积是2,则该反比例函数的解析式为y=$\frac{-4}{x}$.