题目内容
10.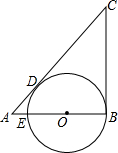 如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )
如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )| A. | 1 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
分析 连接OD,如图,设⊙O的半径为r,先根据切线长定理和切线的性质得CD=CB=8,BC⊥AB,OD⊥AC,再利用勾股定理计算出AB,接着证明△AOD∽△ACB,利用相似比计算出r,然后计算AB-BE就即可.
解答 解:连接OD,如图,设⊙O的半径为r,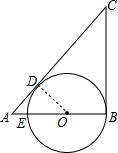
∵CB,CD是⊙O的切线,
∴CD=CB=8,BC⊥AB,OD⊥AC,
在Rt△ABC中,AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∵∠OAD=∠CAB,
∴△AOD∽△ACB,
∴$\frac{OD}{BC}$=$\frac{AD}{AB}$,即$\frac{r}{8}$=$\frac{2}{6}$,解得r=$\frac{8}{3}$,
∴AE=AB-BE=6-2×$\frac{8}{3}$=$\frac{2}{3}$.
故选D.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.解决本题的关键是求出AB的长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列图形中,∠1与∠2是同位角的是( )
| A. | 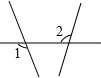 | B. | 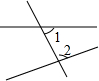 | C. |  | D. | 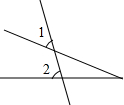 |
20. 如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
 如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )| A. | π | B. | 2π | C. | $\frac{π}{2}$ | D. | 4π |
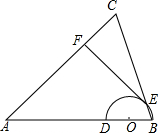 已知:如图,在△ABC中,AB=AC,点O在边AB上,半圆O过点B,且分别与边AB、BC交于点D、E,点D与点A不重合,EF⊥AC,垂足为F.
已知:如图,在△ABC中,AB=AC,点O在边AB上,半圆O过点B,且分别与边AB、BC交于点D、E,点D与点A不重合,EF⊥AC,垂足为F.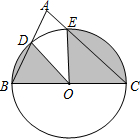 如图.以BC为直径的⊙O与△ABC的另两边分别相交于点D、E,若∠A=50°,BC=6,则图中阴影部分的面积为$\frac{5}{2}$π.
如图.以BC为直径的⊙O与△ABC的另两边分别相交于点D、E,若∠A=50°,BC=6,则图中阴影部分的面积为$\frac{5}{2}$π.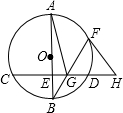 如图.AB为⊙O的直径,CD为⊙O的弦,且AB⊥CD于E,F为劣弧AD上一点,BF交CD于点C,过点F作⊙O的切线,交CD的延长线于H.
如图.AB为⊙O的直径,CD为⊙O的弦,且AB⊥CD于E,F为劣弧AD上一点,BF交CD于点C,过点F作⊙O的切线,交CD的延长线于H.