题目内容
19.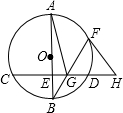 如图.AB为⊙O的直径,CD为⊙O的弦,且AB⊥CD于E,F为劣弧AD上一点,BF交CD于点C,过点F作⊙O的切线,交CD的延长线于H.
如图.AB为⊙O的直径,CD为⊙O的弦,且AB⊥CD于E,F为劣弧AD上一点,BF交CD于点C,过点F作⊙O的切线,交CD的延长线于H.(1)求证:FH=GH;
(2)若AB=2FH=10,tan∠FGH=2,求AG的长.
分析 (1)连接OF,由切线的性质得出∠OFH=90°,由等腰三角形的性质得出∠OFB=∠OBF;由∠HEG、∠EGB都与∠OFB互余可得出两角相等,结合对顶角相等,即可得出∠GFH=∠FGH,由此可证出FH=GH;
(2)过H作HM⊥GF于点M,连接AF,GM=a,AF=b,结合已知条件根据勾股定理即可得出关于a和b的一元一次方程解方程即可求出a,b值;再根据直径对的圆周角为直角,在Rt△AFG中由勾股定理即可得出结论.
解答 (1)证明:连接OF,如图1所示.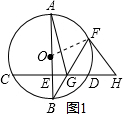
∵HF与⊙O相切于点F,
∴∠OFH=90°,
∴∠GFH=90°-∠OFB.
∵OB=OF,
∴∠OFB=∠OBF.
∵AB⊥CD于E,
∴∠BEG=90°,
∴∠BGE=180°-∠BEG-∠EBG=90°-∠OBF.
∵OB=OF,
∴∠OBF=∠OFB,
∴∠GFH=∠BGE,
又∵∠BGE=∠FGH,
∴∠GFH=∠FGH,
∴FH=GH.
(2)解:过H作HM⊥GF于点M,连接AF,如图2所示.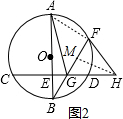
∵AB=2FH=10,tan∠FGH=2,
∴设GM=a,AF=b,
则HM=GF=2a,BF=2b,
由勾股定理得:GH=$\sqrt{G{M}^{2}+H{M}^{2}}$=$\sqrt{5}$a=5,AB=$\sqrt{A{F}^{2}+B{F}^{2}}$=$\sqrt{5}$b=10,
∴a=$\sqrt{5}$,b=2$\sqrt{5}$,
∴AF=2$\sqrt{5}$,GF=2a=2$\sqrt{5}$.
∵AB为直径,
∴∠AFG=90°,
∴AG=$\sqrt{A{F}^{2}+G{F}^{2}}$=
∴AG=$\sqrt{A{E}^{2}+E{G}^{2}}$=2$\sqrt{10}$.
点评 本题考查了切线的性质、勾股定理、等腰三角形的性质以及解直角三角形,解题的关键是:(1)通过边角关系找出∠GFH=∠FGH;(2)通过解直角三角形找出AF、GF的长.本题属于中档题,(1)难度不大;(2)有点难度,解决该问时,通过设未知数解方程得出线段的长度.

 智慧小复习系列答案
智慧小复习系列答案 如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )
如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )| A. | 1 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
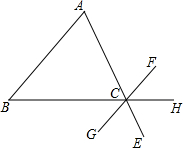 如图所示,请写出一个条件∠B=∠BCG,使AB∥FG.
如图所示,请写出一个条件∠B=∠BCG,使AB∥FG.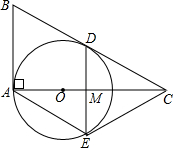 如图,在Rt△ABC中,∠BAC=90°,边AC上有一点O,以点O为圆心,OA长为半径画圆,恰好与边BC相切于点D,过点D作DE⊥AC于点M,DE交⊙O于点E,连接AE,CE.
如图,在Rt△ABC中,∠BAC=90°,边AC上有一点O,以点O为圆心,OA长为半径画圆,恰好与边BC相切于点D,过点D作DE⊥AC于点M,DE交⊙O于点E,连接AE,CE.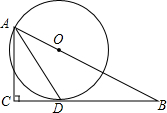 如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.