题目内容
1.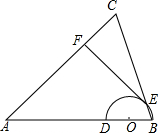 已知:如图,在△ABC中,AB=AC,点O在边AB上,半圆O过点B,且分别与边AB、BC交于点D、E,点D与点A不重合,EF⊥AC,垂足为F.
已知:如图,在△ABC中,AB=AC,点O在边AB上,半圆O过点B,且分别与边AB、BC交于点D、E,点D与点A不重合,EF⊥AC,垂足为F.(1)求证:直线EF是半圆O的切线;
(2)若FC=3,BE=2,OB=2,求BC的长.
分析 (1)根据等腰三角形的性质得到∠C=∠B,∠OEB=∠B,等量代换得到∠C=∠OEB,推出OE∥AC,根据平行线的性质得到OE⊥EF,然后根据切线的判定定理即可得到结论;
(2)根据已知条件得到△BOE是等边三角形,得到∠B=60°,根据直角三角形的性质得到CE=2CF=6,于是得到结论.
解答 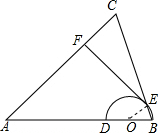 (1)证明:∵AB=AC,
(1)证明:∵AB=AC,
∴∠C=∠B,
∵OB=OE,
∴∠OEB=∠B,
∴∠C=∠OEB,
∴OE∥AC,
∵EF⊥AC,
∴OE⊥EF,
∴直线EF是半圆O的切线;
(2)∵BE=2,OB=2,
∴OB=BE,
∵OE=OB,
∴△BOE是等边三角形,
∴∠B=60°,
∵AC=AB,
∴∠C=∠B=60°,
∵EF⊥AC,
∴∠CEF=30°,
∴CE=2CF=6,
∴BC=CE+BE=8.
点评 本题考查了切线的判定,等腰三角形的性质,等边三角形的判定和性质,直角三角形的性质,平行线的判定和性质,连接OE是解题的关键.

练习册系列答案
相关题目
6.如果?ABCD的周长为40cm,△ABC的周长为25cm,则对角线AC的长是( )
| A. | 5cm | B. | 15cm | C. | 6cm | D. | 16cm |
10.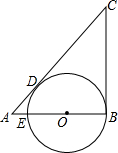 如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )
如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )
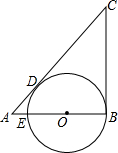 如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )
如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )| A. | 1 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点A,再在河岸的这一边选取点B和点C,使AB⊥BC,然后再选取点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=160m,DC=80m,EC=50m,求A、B间的大致距离.
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点A,再在河岸的这一边选取点B和点C,使AB⊥BC,然后再选取点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=160m,DC=80m,EC=50m,求A、B间的大致距离.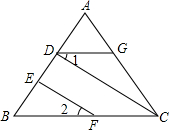 如图,CD⊥AB,EF⊥AB,∠1=∠2,DG与BC平行吗?为什么?
如图,CD⊥AB,EF⊥AB,∠1=∠2,DG与BC平行吗?为什么?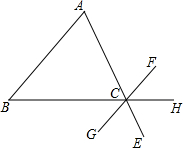 如图所示,请写出一个条件∠B=∠BCG,使AB∥FG.
如图所示,请写出一个条件∠B=∠BCG,使AB∥FG.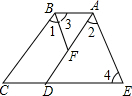 如图,己知∠1=∠2,∠3=∠4,CE∥AB,试说明:AD∥BC.
如图,己知∠1=∠2,∠3=∠4,CE∥AB,试说明:AD∥BC.