题目内容
20.计算:(1)-$\root{3}{2\frac{10}{27}}$
(2)$\root{3}{1-\frac{37}{64}}$
(3)$\root{3}{-27}$+$\sqrt{(-3)^{2}}$-$\root{3}{-1}$
(4)$\sqrt{0.04}$+$\root{3}{-8}$-$\sqrt{\frac{1}{4}}$.
分析 (1)直接利用立方根的定义化简求出答案;
(2)直接利用立方根的定义化简求出答案;
(3)直接利用立方根的定义以及二次根式的性质分别化简求出答案;
(4)直接利用立方根的定义以及二次根式的性质分别化简求出答案.
解答 解:(1)-$\root{3}{2\frac{10}{27}}$=$\root{3}{\frac{64}{27}}$=-$\frac{4}{3}$;
(2)$\root{3}{1-\frac{37}{64}}$=$\root{3}{\frac{27}{64}}$=$\frac{3}{4}$;
(3)$\root{3}{-27}$+$\sqrt{(-3)^{2}}$-$\root{3}{-1}$
=-3+3+1
=1;
(4)$\sqrt{0.04}$+$\root{3}{-8}$-$\sqrt{\frac{1}{4}}$
=0.2-2-$\frac{1}{2}$
=-2.3.
点评 此题主要考查了实数运算,正确利用立方根以及平方根的定义化简是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15. 如图,AB、AC是⊙O的两条弦,∠A=25°,过点C的切线与OB的延长线交于点D,则∠D的度数( )
如图,AB、AC是⊙O的两条弦,∠A=25°,过点C的切线与OB的延长线交于点D,则∠D的度数( )
 如图,AB、AC是⊙O的两条弦,∠A=25°,过点C的切线与OB的延长线交于点D,则∠D的度数( )
如图,AB、AC是⊙O的两条弦,∠A=25°,过点C的切线与OB的延长线交于点D,则∠D的度数( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
10.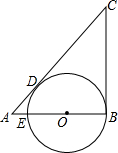 如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )
如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )
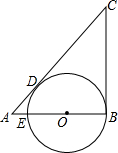 如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )
如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )| A. | 1 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
 如图,已知直线l1,l2,l3被直线l所截,∠1=72°,∠2=108°,∠3=72°,试说明l1∥l2∥l3.
如图,已知直线l1,l2,l3被直线l所截,∠1=72°,∠2=108°,∠3=72°,试说明l1∥l2∥l3. 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点A,再在河岸的这一边选取点B和点C,使AB⊥BC,然后再选取点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=160m,DC=80m,EC=50m,求A、B间的大致距离.
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点A,再在河岸的这一边选取点B和点C,使AB⊥BC,然后再选取点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=160m,DC=80m,EC=50m,求A、B间的大致距离.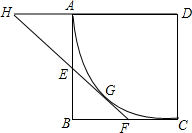 如图,正方形ABCD的边长为6,以D为圆心,DA为半径作⊙D,E在AB上,EF切⊙D于G,交BC于F.
如图,正方形ABCD的边长为6,以D为圆心,DA为半径作⊙D,E在AB上,EF切⊙D于G,交BC于F.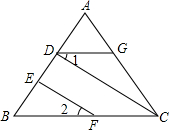 如图,CD⊥AB,EF⊥AB,∠1=∠2,DG与BC平行吗?为什么?
如图,CD⊥AB,EF⊥AB,∠1=∠2,DG与BC平行吗?为什么?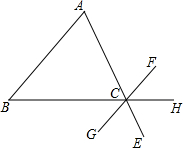 如图所示,请写出一个条件∠B=∠BCG,使AB∥FG.
如图所示,请写出一个条件∠B=∠BCG,使AB∥FG.