题目内容

20．如图，AB为半圆的直径，其AB=4，半圆绕点B顺时针旋转45°，点A旋转到A′的位置，则图中阴影部分的面积为（　　）
A．πB．2πC．$\frac{π}{2}$D．4π

分析 先根据旋转的性质得S半圆AB=S半圆A′B，∠ABA′=45°，再利用面积的和差得到S阴影部分+S半圆AB=S半圆A′B+S扇形ABA′，即有S阴影部分=S扇形ABA′，然后根据扇形的面积公式计算即可．

解答 解：∵半圆AB绕点B顺时针旋转45°，点A旋转到A′的位置，
∴S半圆AB=S半圆A′B，∠ABA′=45°，
∵S阴影部分+S半圆AB=S半圆A′B+S扇形ABA′，
∴S阴影部分=S扇形ABA′=$\frac{45π×{4}^{2}}{360}$=2π．
故选B．

点评 本题考查的是扇形面积的计算，熟记扇形的面积公式是解答此题的关键．

练习册系列答案
相关题目
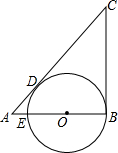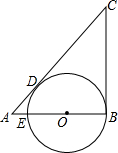10．如图，CB，CD是⊙O的切线，切点分别是B，D，CD的延长线于⊙O的直径BE的延长线交与点A，AD=2，CD=8，则AE的长是（　　）
A．1B．2C．$\frac{1}{3}$D．$\frac{2}{3}$
11．解方程组：
（1）$\left\{\begin{array}{l}3x-y=7①\\ x+3y=-1②\end{array}\right.$；
（2）$\left\{\begin{array}{l}3（x-1）=y+5\\ 5（y-1）=3（x+5）\end{array}\right.$．
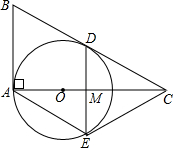8．如图，在Rt△ABC中，∠BAC=90°，边AC上有一点O，以点O为圆心，OA长为半径画圆，恰好与边BC相切于点D，过点D作DE⊥AC于点M，DE交⊙O于点E，连接AE，CE．
（1）求证：CE是⊙O的切线；
（2）若OA=$\sqrt{3}$，DE=3，求证：四边形ABDE是菱形．
15．按要求解下列不等式（组）
（1）2（x+1）-$\frac{x-2}{3}$$＞\frac{7x-2}{2}$
（2）$\left\{\begin{array}{l}{2x-1＜5}\\{\frac{3x-1}{2}+1≥x}\end{array}\right.$
（3）$\left\{\begin{array}{l}{\frac{1-2x}{3}-\frac{4-3x}{6}≥\frac{x-2}{2}}\\{2x-7≤3（x-1）}\end{array}\right.$并把解集在数轴上表示出来．
5．某校260名学生参加植树活动，要求每人植4～7棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵．将各类的人数绘制成扇形图（如图1）和条形图（如图2），经确认扇形图是正确的，而条形图尚有一处错误．
（1）指出条形图中存在的错误，并在原图上改正（涂上阴影）；
（2）在求这20名学生每人植树量的平均数时，小宇是这样分析的：
第一步：此问题中n=4，x1=4，x2=5，x3=6，x4=7；
第二步：求平均数的公式是$\overline{x}$=$\frac{{x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}}{n}$
第三步：$\overline{x}$=$\frac{4+5+6+7}{4}$=5.5
①小宇的分析是从第一步开始出现错误的．
②请你帮他计算出正确的平均数，并估计这260名学生共植树多少棵？
12．如图，在Rt△ABC中，∠ACB=90°，BD是∠ABC的平分线，点O在AB上，⊙O经过B，D两点，交BC于点E．
（1）求证：AC是⊙O的切线；
（2）若AB=9，sin∠BAC=$\frac{2}{3}$，求BE的长．
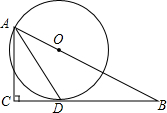9．如图，在Rt△ABC中，∠C=90°，∠BAC的平分线AD交BC边于点D．以AB上一点O为圆心作⊙O，使⊙O经过点A和点D．
（1）求证：直线BC是⊙O的切线；
（2）若AC=3，∠B=30°，求⊙O的半径．
10．解不等式组$\left\{\begin{array}{l}{1-\frac{x-2}{2}≥1}\\{1-2（x-1）＜3}\end{array}\right.$并把解集在数轴上表示出来．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网