题目内容
5.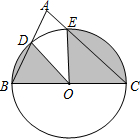 如图.以BC为直径的⊙O与△ABC的另两边分别相交于点D、E,若∠A=50°,BC=6,则图中阴影部分的面积为$\frac{5}{2}$π.
如图.以BC为直径的⊙O与△ABC的另两边分别相交于点D、E,若∠A=50°,BC=6,则图中阴影部分的面积为$\frac{5}{2}$π.
分析 先根据三角形内角和定理得出∠ABC+∠ACB的度数,再由△OBD、△OCE是等腰三角形得出∠BDO+∠CEO的度数,由三角形内角和定理即可得出∠BOD+∠COD的度数,再根据扇形的面积公式即可得出结论.
解答 解:∵△ABC中,∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,
∵△OBD、△OCE是等腰三角形,
∴∠BDO+∠CEO=∠ABC+∠ACB=130°,
∴∠BOD+∠COE=360°-(∠BDO+∠CEO)-(∠ABC+∠ACB)=360°-130°-130°=100°,
∵BC=6,
∴OB=OC=3,
∴S阴影=$\frac{100•π×{3}^{2}}{360}$=$\frac{5}{2}$π.
故答案为:$\frac{5}{2}$π.
点评 本题考查的是扇形面积的计算,解答此类问题时往往用到三角形的内角和是180°这一隐藏条件,要求同学们掌握扇形的面积公式.

练习册系列答案
相关题目
15. 如图,AB、AC是⊙O的两条弦,∠A=25°,过点C的切线与OB的延长线交于点D,则∠D的度数( )
如图,AB、AC是⊙O的两条弦,∠A=25°,过点C的切线与OB的延长线交于点D,则∠D的度数( )
 如图,AB、AC是⊙O的两条弦,∠A=25°,过点C的切线与OB的延长线交于点D,则∠D的度数( )
如图,AB、AC是⊙O的两条弦,∠A=25°,过点C的切线与OB的延长线交于点D,则∠D的度数( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
10.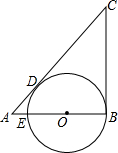 如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )
如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )
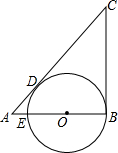 如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )
如图,CB,CD是⊙O的切线,切点分别是B,D,CD的延长线于⊙O的直径BE的延长线交与点A,AD=2,CD=8,则AE的长是( )| A. | 1 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
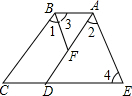 如图,己知∠1=∠2,∠3=∠4,CE∥AB,试说明:AD∥BC.
如图,己知∠1=∠2,∠3=∠4,CE∥AB,试说明:AD∥BC.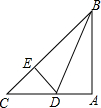 如图,△ABC是等腰直角三角形,∠A=90°,BD是角平分线,DE⊥BC,BC=20,则△DCE的周长为20.
如图,△ABC是等腰直角三角形,∠A=90°,BD是角平分线,DE⊥BC,BC=20,则△DCE的周长为20.