题目内容
8.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个二次三项式,形式如下: -3x+2=x2-5x+1.
-3x+2=x2-5x+1.(1)求所捂的二次三次式;
(2)若请给x选择一个你喜欢的数代入,求所捂二次三项式的值.
分析 (1)根据已知等式,确定出所捂的二次三项式即可;
(2)把x=0代入计算即可求出值.
解答 解:(1)根据题意得:(x2-5x+1)-(-3x+2)=x2-5x+1+3x-2=x2-2x-1;
(2)当x=0时,原式=-1.
点评 此题考查了整式的加减,以及代数式求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.已知:在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l.且a+b-c=m,①填表:②观察下表猜想:m×l=4S.(用含s的代数式表示)③证明②中的结论.
| 三边a、b、c | m | l×m | S |
| 3、4、5 | 2 | 24 | 6 |
| 5、12、13 | 4 | 120 | 30 |
| 8、15、17 | 6 | 240 | 60 |
18.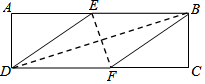 在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE,现给出下列命题:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,则DF=2AD,则( )
在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE,现给出下列命题:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,则DF=2AD,则( )
 在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE,现给出下列命题:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,则DF=2AD,则( )
在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE,现给出下列命题:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,则DF=2AD,则( )| A. | ①是假命题,②是假命题 | B. | ①是真命题,②是假命题 | ||
| C. | ①是假命题,②是真命题 | D. | ①是真命题,②是真命题 |

 已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).
已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0). 如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.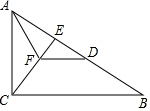 如图,在△ABC中,∠ACB=90°,CE是AB边上的高,AF平分∠CAB交CE于点F,过点F作FD∥CB交AB于点D.求证:AC=AD.
如图,在△ABC中,∠ACB=90°,CE是AB边上的高,AF平分∠CAB交CE于点F,过点F作FD∥CB交AB于点D.求证:AC=AD.