题目内容
11.如图1,点Q为y轴负半轴上的一点,以点Q为圆心的圆交x轴于A、B两点,交y轴于C、D两点,己知点A(-2,0),D(0,-2$\sqrt{3}$),点P为弧$\widehat{ADB}$上一动点.(1)判断△ABD的形状;
(2)如图2,当点P运动时,求$\frac{|PA+PB|}{PC}$的值;
(3)连PD,∠PCD=30°,求$\frac{|PA-PB|}{PC}$的值.

分析 (1)结论:△ABD是等边三角形,只要证明DA=DB,∠OAD=60°即可.
(2)如图2中,作CE⊥PB于E,CF⊥PA于F,连接AC、BC、AD、BD.首先证明Rt△CFA≌Rt△CEB,推出AF=BE,Rt△PCF≌△PCE,推出PF=PE,推出PA+PB=(PF-AF)+(PE+BE)=2PE,因为△ABD是等边三角形,推出∠APB=∠ADB=60°,推出∠APC=∠CPB=30°,根据$\frac{|PA+PB|}{PC}$=$\frac{2PE}{PC}$=2cos30°,即可解决问题.
(3)首先证明∠FCA=∠PCD=30°,PC=2CF,根据$\frac{|PA-PB|}{PC}$=$\frac{2AF}{2FC}$=$\frac{AF}{FC}$=tan30°计算即可解决问题.
解答 解:(1)结论:△ABD是等边三角形,
理由:如图1中,连接AD、BD.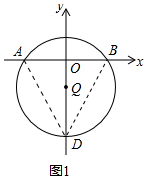
∵QO⊥AB,
∴OA=OB,
∴DA=DB,
∵A(-2,0),D(0,-2$\sqrt{3}$),
∴OA=2,OD=2$\sqrt{3}$,
∴tan∠OAD=$\frac{OD}{OA}$=$\sqrt{3}$,
∴∠OAD=60°,
∴△ABD是等边三角形.
(2)如图2中,作CE⊥PB于E,CF⊥PA于F,连接AC、BC、AD、BD.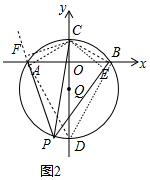
∵QC⊥AB,
∴$\widehat{AC}$=$\widehat{BC}$,AC=BC,
∴∠CPA=∠CPB,
∴CF=CE,
在Rt△CFA和Rt△CEB中,
$\left\{\begin{array}{l}{CF=CE}\\{CA=CB}\end{array}\right.$,
∴Rt△CFA≌Rt△CEB,
∴AF=BE,
同理可证Rt△PCF≌△PCE,
∴PF=PE,
∴PA+PB=(PF-AF)+(PE+BE)=2PE,
∵△ABD是等边三角形,
∴∠APB=∠ADB=60°,
∴∠APC=∠CPB=30°,
∴$\frac{|PA+PB|}{PC}$=$\frac{2PE}{PC}$=2cos30°=$\sqrt{3}$.
(3)由(2)可知:|PA-PB|=(PF-AF)-(PE+BE)|=2AF.
∵∠CPF=∠CDA=30°,∠CAD=∠CFP=90°,
∴∠FCP=∠ACD,
∴∠FCA=∠PCD=30°,
∴PC=2CF,
∴$\frac{|PA-PB|}{PC}$=$\frac{2AF}{2FC}$=$\frac{AF}{FC}$=tan30°=$\frac{\sqrt{3}}{3}$.
点评 本题考查圆综合题、等边三角形的判定和性质、锐角三角函数、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

| A. | x≤0 | B. | x≥0 | C. | x为任何实数 | D. | 以上答案都不对 |
| A. | 在目前位置的北偏东 | B. | 在目前位置的东南方向 | ||
| C. | 距离目前位置900m | D. | 向东走200m,再向北走500m |
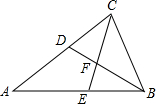 如图,△ABC中,AB=AC,BD、CE分别平分∠ABC和∠ACB,并交于点F,则图中全等三角形共有( )
如图,△ABC中,AB=AC,BD、CE分别平分∠ABC和∠ACB,并交于点F,则图中全等三角形共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
| A. | 由x=y,得到x+2=y+2 | B. | 由2a-3=b-3,得到2a=b | ||
| C. | 由m=n,得到2am=2an | D. | 由am=an,得到m=n |
| A. | |-0.1|<0 | B. | $\frac{4}{3}$<-|-$\frac{5}{4}$| | C. | $\frac{6}{7}$>0.86 | D. | -2=-|-2| |
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不能确定 |
| 品牌 | 月租费 | 本地话费(元/分钟) | 长途话费(元/分钟) |
| 全球通 | 13元 | 0.35 | 0.15 |
| 神州行 | 0元 | 0.60 | 0.30 |
 -3x+2=x2-5x+1.
-3x+2=x2-5x+1.