题目内容
18.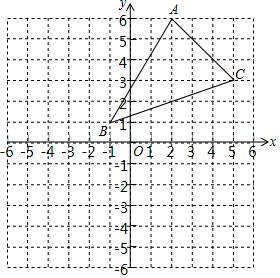 如图,三角形ABC经过平移后,使得点A与点A′(m,5)重合,使得点B与点B′(-5,n)重合.
如图,三角形ABC经过平移后,使得点A与点A′(m,5)重合,使得点B与点B′(-5,n)重合.(1)画出平移后的三角形A′B′C′;
(2)写出平移后的三角形A′B′C′三个顶点的坐标A′(-2,5),B′(-5,0),C′(1,1);
(3)直接写出三角形A′B′C′的面积为13.5.
分析 (1)根据三角形ABC经过平移后,使得点A与点A′(m,5)重合,使得点B与点B′(-5,n)重合,即可得到平移的方向和距离为向下平移1个单位长度,向左平移4个单位长度,据此可得平移后的三角形A′B′C′;
(2)根据平移后的三角形A′B′C′三个顶点的位置,即可得到三角形A′B′C′三个顶点的坐标;
(3)根据割补法进行计算,即可得到三角形A′B′C′的面积.
解答 解:(1)如图所示,三角形A′B′C′即为所求;
(2)由图可得,A′(-2,5),B′(-5,0),C′(1,1),
故答案为:(-2,5),(-5,0),(1,1);
(3)S△A′B′C′=5×6-$\frac{1}{2}$×1×6-$\frac{1}{2}$×3×5-$\frac{1}{2}$×3×4=13.5(平方单位),
故答案为:13.5
点评 本题主要考查了利用平移变换进行作图,解决问题的关键是确定平移的方向和距离,解题时注意:要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.

练习册系列答案
相关题目
9.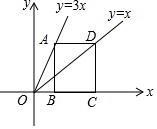 如图,点A、D分别在两条直线y=3x和y=x上,AD∥x轴,已知B、C都在x轴上,且四边形ABCD是矩形,则$\frac{AD}{AB}$的值是( )
如图,点A、D分别在两条直线y=3x和y=x上,AD∥x轴,已知B、C都在x轴上,且四边形ABCD是矩形,则$\frac{AD}{AB}$的值是( )
 如图,点A、D分别在两条直线y=3x和y=x上,AD∥x轴,已知B、C都在x轴上,且四边形ABCD是矩形,则$\frac{AD}{AB}$的值是( )
如图,点A、D分别在两条直线y=3x和y=x上,AD∥x轴,已知B、C都在x轴上,且四边形ABCD是矩形,则$\frac{AD}{AB}$的值是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 3 | D. | $\frac{3}{2}$ |
 已知某市2017年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图所示.
已知某市2017年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图所示. 如图,若∠1=∠D=40°,∠C和∠D互余,求∠B的度数.
如图,若∠1=∠D=40°,∠C和∠D互余,求∠B的度数.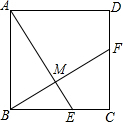 如图,正方形ABCD中,点E、F分别是边BC、CD上的点,且BE=CF,求证:
如图,正方形ABCD中,点E、F分别是边BC、CD上的点,且BE=CF,求证: