题目内容
 在正方形ABCD中,E为AD上的中点,F是AB的四分等分点.连接EF,EC,△AEF与△DCE是否相似?请说明理由.
在正方形ABCD中,E为AD上的中点,F是AB的四分等分点.连接EF,EC,△AEF与△DCE是否相似?请说明理由.考点:相似三角形的判定
专题:
分析:设正方形的边长为a,则AE=DE=
a,AF=
a,再由
=
即可得出结论.
| 1 |
| 2 |
| 1 |
| 4 |
| AE |
| AF |
| CD |
| DE |
解答:解:△AEF∽△DCE.
∵四边形ABCD是正方形,
∴∠A=∠D=90°.
设正方形的边长为a,则AE=DE=
a,AF=
a,
∵
=
=2,
=
=2,
∴
=
,
∴△AEF∽△DCE.
∵四边形ABCD是正方形,
∴∠A=∠D=90°.
设正方形的边长为a,则AE=DE=
| 1 |
| 2 |
| 1 |
| 4 |
∵
| AE |
| AF |
| ||
|
| CD |
| DE |
| a | ||
|
∴
| AE |
| AF |
| CD |
| DE |
∴△AEF∽△DCE.
点评:本题考查的是相似三角形的判定,熟知两组对应边的比相等且夹角对应相等的两个三角形相似是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
甲乙两地相距150千米,一辆小汽车和一辆客车同时从两地相向开出,经过50分钟相遇,此时小汽车比客车多行驶30千米.设小汽车和客车的平均速度分别为x千米/小时和y千米/小时.则下列方程组正确的是( )
A、
| |||||||||||||
B、
| |||||||||||||
C、
| |||||||||||||
D、
|

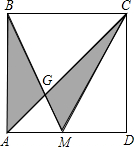 如图,正方形ABCD的面积为1,M是AD的中点,求图中阴影部分的面积.
如图,正方形ABCD的面积为1,M是AD的中点,求图中阴影部分的面积. 如图,在△ABC中,以AC为直径的⊙O交BC于D,过C作⊙O的切线,交AB的延长线于P,∠PCB=
如图,在△ABC中,以AC为直径的⊙O交BC于D,过C作⊙O的切线,交AB的延长线于P,∠PCB= 如图,在四边形ABCD中,AB⊥BC,AD⊥DC,连接BD,AC,且DE⊥AC于E,交AB于F,求证:△AFD∽△ADB.
如图,在四边形ABCD中,AB⊥BC,AD⊥DC,连接BD,AC,且DE⊥AC于E,交AB于F,求证:△AFD∽△ADB. 如图,已知△ABC中AB=AC,BD、CD分别平分∠EBA、∠ECA,BD交AC于F,连接AD,
如图,已知△ABC中AB=AC,BD、CD分别平分∠EBA、∠ECA,BD交AC于F,连接AD, 如图,两个同心圆被两条半径截得
如图,两个同心圆被两条半径截得
 如图,∠B=40°,∠C=20°,∠CDB=3∠A,求∠A的度数.
如图,∠B=40°,∠C=20°,∠CDB=3∠A,求∠A的度数.