题目内容
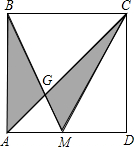 如图,正方形ABCD的面积为1,M是AD的中点,求图中阴影部分的面积.
如图,正方形ABCD的面积为1,M是AD的中点,求图中阴影部分的面积.考点:正方形的性质
专题:
分析:由条件可得到AM:BC=1:2,可找到△BAG和△BAM的关系,结合正方形的面积,可求得△BAE的面积,且△BAG和△CMG的面积相等,可求得阴影部分的面积.
解答:解:∵M为AD中点,
∴AM=MD,则AM=
AD=
BC,即AM:BC=1:2,
则MG:BG=1:2,S△BAG=
S△BAM,
又∵S△BAM=
S正方形ABCD,
则S△BAG=
×
S正方形ABCD,
=
,
而S△BAG=S△GMC,
所以阴影部分的面积为:
×2=
;
∴图中阴影部分的面积是
.
∴AM=MD,则AM=
| 1 |
| 2 |
| 1 |
| 2 |
则MG:BG=1:2,S△BAG=
| 2 |
| 3 |
又∵S△BAM=
| 1 |
| 4 |
则S△BAG=
| 2 |
| 3 |
| 1 |
| 4 |
=
| 1 |
| 6 |
而S△BAG=S△GMC,
所以阴影部分的面积为:
| 1 |
| 6 |
| 1 |
| 3 |
∴图中阴影部分的面积是
| 1 |
| 3 |
点评:本题主要考查正方形的性质,利用正方形的四边相等、对边平行找到△BAM和△BAG的关系是解题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 在?ABCD中,对角线AC=8,BD=6,AC和BD的夹角为α,当α=45°时,?ABCD的面积为
在?ABCD中,对角线AC=8,BD=6,AC和BD的夹角为α,当α=45°时,?ABCD的面积为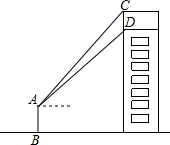 如图,某数学课外活动小组利用课余时间,测量了安装在一幢楼房顶部的公益广告牌的高,如图,DM为楼房的高,且C,D,M三点共线,在楼房的侧面A处,测得点C与点D的仰角分别为45°和37.3°,BM=15米,根据以上测得的相关数据,求这个广告牌的高(CD的长)(结果精确到0.1米,参考数据:sin37.3°≈0.606.cos37.3≈0.7955,tan37.3°≈0.7618)
如图,某数学课外活动小组利用课余时间,测量了安装在一幢楼房顶部的公益广告牌的高,如图,DM为楼房的高,且C,D,M三点共线,在楼房的侧面A处,测得点C与点D的仰角分别为45°和37.3°,BM=15米,根据以上测得的相关数据,求这个广告牌的高(CD的长)(结果精确到0.1米,参考数据:sin37.3°≈0.606.cos37.3≈0.7955,tan37.3°≈0.7618)
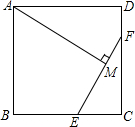 已知:E,F分别是正方形ABCD的边BC,CD上的点,AM⊥EF,垂足为M,AM=AB,
已知:E,F分别是正方形ABCD的边BC,CD上的点,AM⊥EF,垂足为M,AM=AB, 如图,线段AD、BC相交于点E,AB⊥BC,BC⊥DC,BE=120,EC=60,DC=50,求AB的长.
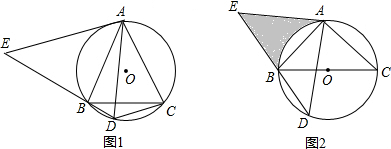
如图,线段AD、BC相交于点E,AB⊥BC,BC⊥DC,BE=120,EC=60,DC=50,求AB的长. 如图.菱形ABCD中.点E为AC上一点,且DE⊥BE.
如图.菱形ABCD中.点E为AC上一点,且DE⊥BE. 在正方形ABCD中,E为AD上的中点,F是AB的四分等分点.连接EF,EC,△AEF与△DCE是否相似?请说明理由.
在正方形ABCD中,E为AD上的中点,F是AB的四分等分点.连接EF,EC,△AEF与△DCE是否相似?请说明理由.