题目内容
 如图,两个同心圆被两条半径截得
如图,两个同心圆被两条半径截得 |
| AB |
 |
| CD |
考点:扇形面积的计算,弧长的计算
专题:
分析:先设OC=r,则OA=r+12,∠AOB=n°,由弧长公式可求出n、r的值,再根据S阴影=S扇形AOB-S扇形COD即可得出结论.
解答:解:设OC=r,则OA=r+12,∠AOB=n°,
∴lAB=
=10π,lCD=
=6π,
∴
,
∴OC=18,OA=OC+AC=30,
∴S阴影=S扇形AOB-S扇形COD=
•OA-
•OC
=
×10π×30-
×6π×18
=96π.
∴lAB=
| nπ(r+12) |
| 180 |
| nπr |
| 180 |
∴
|
∴OC=18,OA=OC+AC=30,
∴S阴影=S扇形AOB-S扇形COD=
| 1 |
| 2 |
 |
| AB |
| 1 |
| 2 |
 |
| CD |
=
| 1 |
| 2 |
| 1 |
| 2 |
=96π.
点评:本题考查了扇形面积的计算及弧长公式,根据题意得出S阴影=S扇形AOB-S扇形COD是解答此题的关键.

练习册系列答案
相关题目
在下列现象中,属于平移的是( )
| A、冰化为水 |
| B、电梯由一楼升到八楼 |
| C、导弹击中目标后爆炸 |
| D、卫星绕地球运动 |
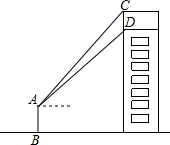 如图,某数学课外活动小组利用课余时间,测量了安装在一幢楼房顶部的公益广告牌的高,如图,DM为楼房的高,且C,D,M三点共线,在楼房的侧面A处,测得点C与点D的仰角分别为45°和37.3°,BM=15米,根据以上测得的相关数据,求这个广告牌的高(CD的长)(结果精确到0.1米,参考数据:sin37.3°≈0.606.cos37.3≈0.7955,tan37.3°≈0.7618)
如图,某数学课外活动小组利用课余时间,测量了安装在一幢楼房顶部的公益广告牌的高,如图,DM为楼房的高,且C,D,M三点共线,在楼房的侧面A处,测得点C与点D的仰角分别为45°和37.3°,BM=15米,根据以上测得的相关数据,求这个广告牌的高(CD的长)(结果精确到0.1米,参考数据:sin37.3°≈0.606.cos37.3≈0.7955,tan37.3°≈0.7618) 如图.菱形ABCD中.点E为AC上一点,且DE⊥BE.
如图.菱形ABCD中.点E为AC上一点,且DE⊥BE. 在正方形ABCD中,E为AD上的中点,F是AB的四分等分点.连接EF,EC,△AEF与△DCE是否相似?请说明理由.
在正方形ABCD中,E为AD上的中点,F是AB的四分等分点.连接EF,EC,△AEF与△DCE是否相似?请说明理由. 某宾馆要在一高BC=3m、长AB=5m、宽3m的楼梯上铺设地毯,楼梯的刨面如图所示.若地毯每平方米100元,则需要购买地毯的费用至少是
某宾馆要在一高BC=3m、长AB=5m、宽3m的楼梯上铺设地毯,楼梯的刨面如图所示.若地毯每平方米100元,则需要购买地毯的费用至少是 如图所示,直线EF上有两点A,C,分别引两条射线AB,CD,∠BAF=110°,∠DCF=60°,射线AB,CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t,在射线CD移动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.
如图所示,直线EF上有两点A,C,分别引两条射线AB,CD,∠BAF=110°,∠DCF=60°,射线AB,CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t,在射线CD移动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.