题目内容
如图，在四边形ABCD中，AB⊥BC，AD⊥DC，连接BD，AC，且DE⊥AC于E，交AB于F，求证：△AFD∽△ADB．考点：相似三角形的判定
专题：证明题
分析：先根据题意得出△EAF∽△BAC，△AED∽△ADC，再由相似三角形的对应边成比例可得出
=
，再由∠DAF=∠BAD即可得出结论．
| AD |
| AF |
| AB |
| AD |
解答：证明：∵∠AEF=∠ABC=90°，∠EAF=∠BAC．
∴△EAF∽△BAC，
=
，即AE•AC=AF•AB．
同理可得，△AED∽△ADC，
=
，即AE•AC=AD2，
∴AD2=AF•AB，即
=
，
又∵∠DAF=∠BAD，
∴△AFD∽△ADB．
∴△EAF∽△BAC，
| AE |
| AB |
| AF |
| AC |
同理可得，△AED∽△ADC，
| AE |
| AD |
| AD |
| AC |
∴AD2=AF•AB，即
| AD |
| AF |
| AB |
| AD |
又∵∠DAF=∠BAD，
∴△AFD∽△ADB．
点评：本题考查的是相似三角形的判定，熟知两组对应边的比相等且夹角对应相等的两个三角形相似是解答此题的关键．
练习册系列答案
相关题目
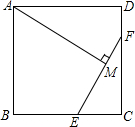已知：E，F分别是正方形ABCD的边BC，CD上的点，AM⊥EF，垂足为M，AM=AB，
如图．菱形ABCD中．点E为AC上一点，且DE⊥BE．
如图，在△ABC中，AB=AC，∠BAC=90°，BC=8，⊙A与BC相切于点D，且与AB、AC分别交于点E、F，则劣弧
在正方形ABCD中，E为AD上的中点，F是AB的四分等分点．连接EF，EC，△AEF与△DCE是否相似？请说明理由．
某宾馆要在一高BC=3m、长AB=5m、宽3m的楼梯上铺设地毯，楼梯的刨面如图所示．若地毯每平方米100元，则需要购买地毯的费用至少是
如图所示，直线EF上有两点A，C，分别引两条射线AB，CD，∠BAF=110°，∠DCF=60°，射线AB，CD分别绕A点，C点以1度/秒和3度/秒的速度同时顺时针转动，设时间为t，在射线CD移动一周的时间内，是否存在某时刻，使得CD与AB平行？若存在，求出所有满足条件的时间t．
如图所示，南北方向QP为我国的领海线，以西为公海，晚上10点28分，我边防反偷渡巡逻艇122号在A处发现其正西方向有一只可疑船只C之间的距离为10海里，A、B两艇之间的距离为6海里，B艇与可疑船只C之间的距离为8海里，若该可疑船只的速度为12.8海里/时，问该可疑船只最早在何时进入我国领海？