题目内容
17. 已知二次函数y=x2+bx+c的图象与y轴交于点C(0,-3),与x轴的一个交点坐标是A(-1,0).
已知二次函数y=x2+bx+c的图象与y轴交于点C(0,-3),与x轴的一个交点坐标是A(-1,0).(1)求二次函数的解析式,并写出顶点D的坐标;
(2)将二次函数的图象沿x轴向左平移$\frac{3}{2}$个单位长度,当y<0时,求x的取值范围.
分析 (1)将点A和点C的坐标代入抛物线的解析式可求得b、c的值,从而得到抛物线的解析式,然后依据配方法可求得抛物线的顶点坐标;
(2)依据抛物线的解析式与平移的规划规律,写出平移后抛物线的解析式,然后求得抛物线与x轴的交点坐标,最后依据y<0可求得x的取值范围.
解答 解:
(1)∵把C(0,-3)代入抛物线的解析式得:C=-3,把A(-1,0)代入y=x2+bx-3得:b=-2,
∴抛物线的解析式为y=x2-2x-3.
∴y=(x-1)2-4.
∴抛物线的顶点坐标D(1,-4);
(2)二次函数的图形沿x轴向左平移$\frac{3}{2}$个单位长度得:y=(x-1+$\frac{3}{2}$)2-4=(x+$\frac{1}{2}$)2-4,
令y=0得:(x+$\frac{1}{2}$)2-4=0,解得:x1=$\frac{3}{2}$,x2=-$\frac{5}{2}$.
∵a>0,
∴当y<0时,x的取值范围是-$\frac{5}{2}$<x<$\frac{3}{2}$.
点评 本题主要考查的是抛物线与x轴的交点、待定系数法求二次函数的解析式,掌握相关知识是解题的关键.

练习册系列答案
相关题目
9.已知点A(-1-$\sqrt{2}$,y1)、B(-1,y2)、C(2,y3)在抛物线y=(x-1)2+c上,则y1、y2、y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y1>y2 | D. | y2>y3>y1 |
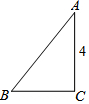 如图,在Rt△ABC中,∠C=90°,AC=4,cosA=$\frac{4}{5}$,则BC=3.
如图,在Rt△ABC中,∠C=90°,AC=4,cosA=$\frac{4}{5}$,则BC=3.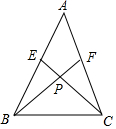 如图,AB=AC,AE=AF.
如图,AB=AC,AE=AF.