题目内容
8.解方程(1)4(x-2)2-81=0.
(2)x2-3x+2=0.
分析 (1)先把方程变形为)(x-2)2=$\frac{81}{4}$,然后利用直接开平方法解方程;
(2)利用因式分解法解方程.
解答 解:(1)(x-2)2=$\frac{81}{4}$,
x-2=±$\frac{9}{2}$,
所以x1=$\frac{13}{2}$,x2=-$\frac{5}{2}$;
(2)(x-2)(x-1)=0,
x-2=0或x-1=0,
所以x1=2,x2=1.
点评 本题考查了解一元二次方程-因式分解法:就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了直接开平方法解一元二次方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12. 如图,某同学把一块三角形玻璃打碎了,现要去买一块大小形状完全相同的玻璃,那么最省事的办法是( )
如图,某同学把一块三角形玻璃打碎了,现要去买一块大小形状完全相同的玻璃,那么最省事的办法是( )
 如图,某同学把一块三角形玻璃打碎了,现要去买一块大小形状完全相同的玻璃,那么最省事的办法是( )
如图,某同学把一块三角形玻璃打碎了,现要去买一块大小形状完全相同的玻璃,那么最省事的办法是( )| A. | 带①和②去 | B. | 带①去 | C. | 带②去 | D. | 带③去 |
20.甲乙两辆汽车在一条公路上匀速行驶,为了确定汽车的位置,我们用数轴表示这条公路,并规定向右为正方向,原点O为0km路标.并作如下约定:位置为正,表示汽车位于零千米右侧;位置为负,表示汽车位于零千米左侧,位置为零,表示汽车位于零千米处.
(1)根据题意,填写下列表格:
(2)甲、乙两车能否相遇,如能相遇,求出相遇时间及相遇时的位置;如不能,说明理由;
(3)甲、乙两车能否相距120km,若能,求出两车相距120km时的时间;若不能,请说明理由.
(1)根据题意,填写下列表格:
| 时间(h) | 0 | 3 | 5 | x |
| 甲车位置(km) | 150 | -30 | -150 | 150-60x |
| 乙车位置(km) | -50 | 70 | 150 | -50+40x |
(3)甲、乙两车能否相距120km,若能,求出两车相距120km时的时间;若不能,请说明理由.
18.对于抛物线y=$\frac{1}{2}$(x+2)2+1的下列描述中,错误是( )
| A. | 对称轴为x=-2,顶点坐标为(-2,1) | |
| B. | 当x<-2时,函数值y随x值的增大而减小 | |
| C. | 当x=2时,有最大值为1 | |
| D. | 当x>-2时,函数值y随x值的增大而增大 |
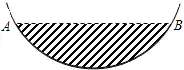 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面. 已知二次函数y=x2+bx+c的图象与y轴交于点C(0,-3),与x轴的一个交点坐标是A(-1,0).
已知二次函数y=x2+bx+c的图象与y轴交于点C(0,-3),与x轴的一个交点坐标是A(-1,0).