题目内容
7.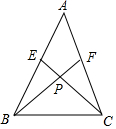 如图,AB=AC,AE=AF.
如图,AB=AC,AE=AF.(1)求证:PB=PC;
(2)写出图中相等的其它线段.
分析 (1)可证明△ABF≌△ACE,则BF=CE,再证明△BEP≌△CFP,则PB=PC,
(2)利用全等三角形的性质进而得出PE=PF,BE=CF.
解答 证明:(1)在△ABF和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAF=∠CAE}\\{AF=AE}\end{array}\right.$,
∴△ABF≌△ACE(SAS),
∴∠ABF=∠ACE(全等三角形的对应角相等),
∴BF=CE(全等三角形的对应边相等),
∵AB=AC,AE=AF,
∴BE=CF,
在△BEP和△CFP中,
$\left\{\begin{array}{l}{∠BPE=∠CPF}\\{∠PBE=∠PCF}\\{BE=CF}\end{array}\right.$,
∴△BEP≌△CFP(AAS),
∴PB=PC,
(2)∵BF=CE,
∴PE=PF,
∴图中相等的线段为PE=PF,BE=CF,BF=CE
点评 本题考查了全等三角形的判定和性质以及等腰三角形的性质,关键是证明△ABF≌△ACE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.对于抛物线y=$\frac{1}{2}$(x+2)2+1的下列描述中,错误是( )
| A. | 对称轴为x=-2,顶点坐标为(-2,1) | |
| B. | 当x<-2时,函数值y随x值的增大而减小 | |
| C. | 当x=2时,有最大值为1 | |
| D. | 当x>-2时,函数值y随x值的增大而增大 |
15.2016年9月28第七届安徽省花博会在阜阳开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的柳编工艺品投放市场进行试销.阜阳市物价部门规定该工艺品销售单价不得低于成本价,最高不能超过38元/件,经过调查,得到如表数据:
(1)若y与x是一次函数关系y=kx+b,求这个一次函数关系式;
(2)当销售单价定为多少时,该厂试销该工艺品每天所获利润最大?最大利润是多少?
(3)若该工艺厂要获得的利润不低于8000元,试确定销售单价x的取值范围.
| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 500 | 400 | 300 | 200 | 100 | … |
(2)当销售单价定为多少时,该厂试销该工艺品每天所获利润最大?最大利润是多少?
(3)若该工艺厂要获得的利润不低于8000元,试确定销售单价x的取值范围.
2.某摩托车厂本周计划每日生产250辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划相比情况如表(增加的辆数为正数,减少的辆数为负数):
请你利用正负数求出本周总生产量.
| 星期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 产量变化/辆 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
 已知二次函数y=x2+bx+c的图象与y轴交于点C(0,-3),与x轴的一个交点坐标是A(-1,0).
已知二次函数y=x2+bx+c的图象与y轴交于点C(0,-3),与x轴的一个交点坐标是A(-1,0).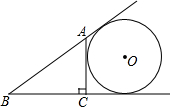 如图,AC⊥BC于点C,⊙O与直线AB、BC、CA都相切,若BC=3,△ABC的周长是10,则⊙O的半径等于2.
如图,AC⊥BC于点C,⊙O与直线AB、BC、CA都相切,若BC=3,△ABC的周长是10,则⊙O的半径等于2.