题目内容
6.在三角形ABC中,若∠A=$\frac{1}{2}$∠B,∠C=3∠A,则三角形ABC是什么三角形.分析 根据三角形内角和定理列出算式,求出∠A=30°,∠C=90°,即可判断.
解答 解:∵∠A=$\frac{1}{2}$∠B,∠C=3∠A,
∴∠B=2∠A,
由三角形内角和定理得,∠A+2∠A+3∠A=180°
则6∠A=180°,
解得,∠A=30°,
∴∠B=2∠A=2×30°=60°,∠C=3∠A=3×30°=90°,
∴△ABC是直角三角形.
点评 本题考查的是三角形内角和定理,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
18.对于抛物线y=$\frac{1}{2}$(x+2)2+1的下列描述中,错误是( )
| A. | 对称轴为x=-2,顶点坐标为(-2,1) | |
| B. | 当x<-2时,函数值y随x值的增大而减小 | |
| C. | 当x=2时,有最大值为1 | |
| D. | 当x>-2时,函数值y随x值的增大而增大 |
15.2016年9月28第七届安徽省花博会在阜阳开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的柳编工艺品投放市场进行试销.阜阳市物价部门规定该工艺品销售单价不得低于成本价,最高不能超过38元/件,经过调查,得到如表数据:
(1)若y与x是一次函数关系y=kx+b,求这个一次函数关系式;
(2)当销售单价定为多少时,该厂试销该工艺品每天所获利润最大?最大利润是多少?
(3)若该工艺厂要获得的利润不低于8000元,试确定销售单价x的取值范围.
| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 500 | 400 | 300 | 200 | 100 | … |
(2)当销售单价定为多少时,该厂试销该工艺品每天所获利润最大?最大利润是多少?
(3)若该工艺厂要获得的利润不低于8000元,试确定销售单价x的取值范围.
 已知二次函数y=x2+bx+c的图象与y轴交于点C(0,-3),与x轴的一个交点坐标是A(-1,0).
已知二次函数y=x2+bx+c的图象与y轴交于点C(0,-3),与x轴的一个交点坐标是A(-1,0).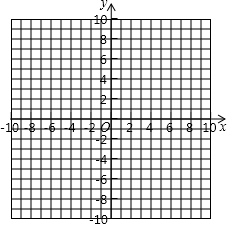 在如图的平面直角坐标系中作△ABC,使点A、B、C的坐标分别为A(4,6),B(0,2),C(6,0),并作出△ABC关于y轴的对称图形.
在如图的平面直角坐标系中作△ABC,使点A、B、C的坐标分别为A(4,6),B(0,2),C(6,0),并作出△ABC关于y轴的对称图形.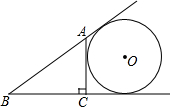 如图,AC⊥BC于点C,⊙O与直线AB、BC、CA都相切,若BC=3,△ABC的周长是10,则⊙O的半径等于2.
如图,AC⊥BC于点C,⊙O与直线AB、BC、CA都相切,若BC=3,△ABC的周长是10,则⊙O的半径等于2.